
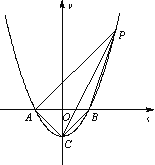
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
⑴ 求![]() 、
、![]() 、
、![]() 三点的坐标.
三点的坐标.
⑵ 过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
⑶ 在![]() 轴上方的抛物线上是否存在一点
轴上方的抛物线上是否存在一点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() , 使以
, 使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似.若存在,请求出
相似.若存在,请求出![]() 点的坐标;否则,请说明理由.
点的坐标;否则,请说明理由.
【答案】(1)![]() (2)
(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)令![]() 可分别求出
可分别求出![]() 的坐标;(2)对四边形
的坐标;(2)对四边形![]() 的面积进行分割成
的面积进行分割成![]() 再分别求解;(3)假设存在,分
再分别求解;(3)假设存在,分![]() 为直角两种情况讨论,利用相似求解.
为直角两种情况讨论,利用相似求解.
试题解析:⑴![]() ,
,![]() ,
,![]()
⑵ ∵![]() ∴
∴![]()
∵![]() ∴
∴![]() .
.
过点![]() 作
作![]() 轴于
轴于![]() ,则
,则![]() 为等腰直角三角形.
为等腰直角三角形.
令![]() ,则
,则![]() .∴
.∴![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上.
上.
∴![]() 解得
解得![]() ,
,![]() (不合题意,舍去)∴
(不合题意,舍去)∴![]() .
.
∴四边形![]() 的面积
的面积![]() .
.
⑶ 假设存在
∵![]() ∴
∴![]() .
.
∵![]() 轴于点
轴于点![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ∴
∴![]()
在![]() 中,
中,![]() ∴
∴![]()
设![]() 点的横坐标为
点的横坐标为![]() ,则
,则![]()
①点![]() 在
在![]() 轴左侧时,则
轴左侧时,则![]() .
.
(ⅰ)当![]() 时,有
时,有![]() .
.
∵![]() ,
,![]() .即
.即![]() .解得
.解得![]() (舍去)
(舍去)![]() (舍去).
(舍去).
(ⅱ)当![]() 时,有
时,有![]() ,即
,即![]() .
.
解得:![]() (舍去)
(舍去)![]() . ∴
. ∴![]()
② 点![]() 在
在![]() 轴右侧时,则
轴右侧时,则![]() .
.
(ⅰ)当![]() 时有
时有![]() .
.
∵![]() ,∴
,∴![]() ,
,
解得![]() (舍去),
(舍去),![]() .∴
.∴![]()
(ⅱ)当![]() 时有
时有![]() .即
.即![]() .
.
解得:![]() (舍去)
(舍去)![]() .∴
.∴![]()
∴存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似.
相似.
![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
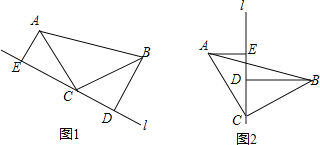
【题目】如图,△ABC中,∠ACB=90°,AC=BC,直线l过点C,BD⊥l,AE⊥l,垂足分别为D、E.
(1)当直线l不与底边AB相交时,求证:ED=AE+BD;
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB相交时,请你探究ED、AE、BD三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
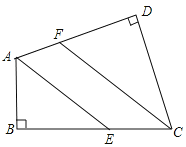
【题目】已知:如图,四边形ABCD中,AD⊥DC,BC⊥AB,AE平分∠BAD,CF平分∠DCB,AE交CD于E,CF交AB于F,问AE与CF是否平行?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连结BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC其中结论正确的个数有( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com