
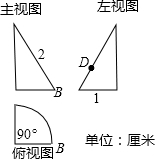
 如图是一个锥体的三视图.
如图是一个锥体的三视图.分析 (1)由锥体的三视图可得出结论;
(2)根据勾股定理求出主视图中三角形的高,锥体的表面积=侧面积+底面积,将数值带入即可得出结论;
(3)画出锥体的侧面展开图,根据勾股定理即可得出结论.
解答 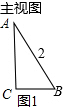 解:(1)如图1,由三视图可知,该锥体是以AC为轴,以点C为旋转中心,旋转90°形成的;
解:(1)如图1,由三视图可知,该锥体是以AC为轴,以点C为旋转中心,旋转90°形成的;
(2)AC=$\sqrt{{2}^{2}{-1}^{2}}$=$\sqrt{3}$
S表面积=S底+S侧=$\frac{1}{4}$π×12+(2×$\frac{1}{2}$×1×$\sqrt{3}$+$\frac{90π×{2}^{2}}{360}$)=$\frac{π}{4}$+$\sqrt{3}$+π=$\sqrt{3}$+$\frac{5π}{4}$.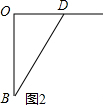 (3)如图2所示,
(3)如图2所示,
∵OD=1,OB=2,
∴BD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
点评 本题主要考查锥体三视图,把立体图形转化为平面图形的思维,是解决本题的关键.


科目:初中数学 来源: 题型:解答题
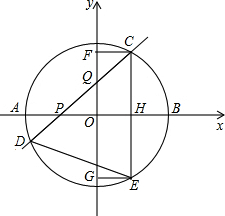 如图,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为y=x+m,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
如图,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为y=x+m,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
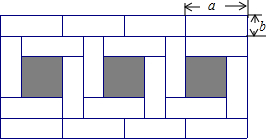 已知将同样大小的小长方形纸片拼成的如图形状的大长方形(小长方形纸片长为a,宽为b)请你仔细观察图形,解答下列问题:
已知将同样大小的小长方形纸片拼成的如图形状的大长方形(小长方形纸片长为a,宽为b)请你仔细观察图形,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
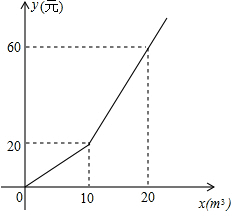 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.| 每月用水量 (m3) | 单价(元/m3) |
| 不超出10m3的部分 | a |
| 超出10m3的部分 | a+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
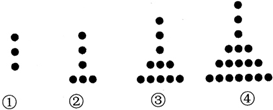
| A. | 26 | B. | 37 | C. | 38 | D. | 51 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
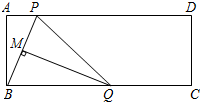 如图,在矩形ABCD中,点P是边AD上的动点,连结BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连结QP.已知AD=13,AB=5,设AP=x,BQ=y.
如图,在矩形ABCD中,点P是边AD上的动点,连结BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连结QP.已知AD=13,AB=5,设AP=x,BQ=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
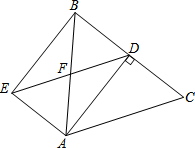 如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积.
如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com