
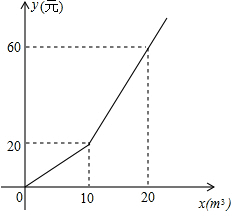
 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.| 每月用水量 (m3) | 单价(元/m3) |
| 不超出10m3的部分 | a |
| 超出10m3的部分 | a+2 |
分析 (1)根据图象可得用水是10m3时水费是20元,据此求得a的值,利用待定系数法求得y与x的函数解析式;
(2)设三月份用水zm3,则四月份用水(20-z)m3,根据共交水费52元,即可列方程求解.
解答 解:(1)a=$\frac{20}{10}$=2.
当0≤x≤10时,函数解析式是y=2x;
当10<x≤20时,设y=kx+b,
则$\left\{\begin{array}{l}{10k+b=20}\\{20k+b=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=4}\\{b=-20}\end{array}\right.$.
则函数解析式是y=4x-20;
(2)设三月份用水zm3,则四月份用水(20-z)m3,
根据题题意得:2z+4(20-z)-10=52,
解得:z=9,
则20-9=11(m3).
答:三月份用水9m3,四月份用水11m3.
点评 本题考查了一次函数的应用,以及待定系数法求函数的解析式,注意到四月份用水量超过三月份,则三月份用水不足10m3,而四月份超过10m3,是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种板材(m2/套) | 乙种板材(m2/套) | 获利(元/套) | |
| A款 | 3 | 7 | 600 |
| B款 | 5 | 3 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
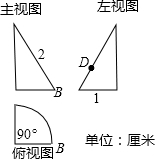 如图是一个锥体的三视图.
如图是一个锥体的三视图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com