
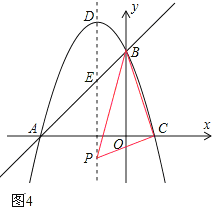
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
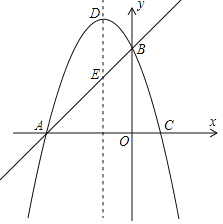
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
【答案】(1)y=﹣x2﹣2x+3
(2)点F的坐标为(![]() ,
,![]() )
)
(3)当t为![]() 秒或2秒或3秒或
秒或2秒或3秒或![]() 秒时,以P、B、C为顶点的三角形是直角三角形。
秒时,以P、B、C为顶点的三角形是直角三角形。
【解析】
试题(1)先由直线AB的解析式为y=x+3,求出它与x轴的交点A、与y轴的交点B的坐标,再将A、B两点的坐标代入y=﹣x2+bx+c,运用待定系数法即可求出抛物线的解析式。
∵y=x+3与x轴交于点A,与y轴交于点B,
∴当y=0时,x=﹣3,即A点坐标为(﹣3,0),当x=0时,y=3,即B点坐标为(0,3)。
将A(﹣3,0),B(0,3)代入y=﹣x2+bx+c,得
![]() ,解得
,解得![]() 。
。
∴抛物线的解析式为y=﹣x2﹣2x+3。
(2)设第三象限内的点F的坐标为(m,﹣m2﹣2m+3),运用配方法求出抛物线的对称轴及顶点D的坐标,再设抛物线的对称轴与x轴交于点G,连接FG,根据S△AEF=S△AEG+S△AFG﹣S△EFG=3,列出关于m的方程,解方程求出m的值,进而得出点F的坐标。
如图1,设第三象限内的点F的坐标为(m,﹣m2﹣2m+3),
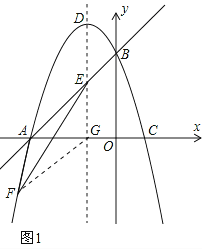
则m<0,﹣m2﹣2m+3<0。
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴对称轴为直线x=﹣1,顶点D的坐标为(﹣1,4)。
设抛物线的对称轴与x轴交于点G,连接FG,
则G(﹣1,0),AG=2。
∵直线AB的解析式为y=x+3,
∴当x=﹣1时,y=﹣1+3=2。∴E点坐标为(﹣1,2)。
∵S△AEF=S△AEG+S△AFG﹣S△EFG
=![]() ×2×2+
×2×2+![]() ×2×(m2+2m﹣3)﹣
×2×(m2+2m﹣3)﹣![]() ×2×(﹣1﹣m)=m2+3m,
×2×(﹣1﹣m)=m2+3m,
∴以A、E、F为顶点的三角形面积为3时,m2+3m=3,
解得m1=![]() ,m2=
,m2=![]() (舍去)。
(舍去)。
当m=![]() 时,﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m=
时,﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m=![]() 。
。
∴点F的坐标为(![]() ,
,![]() )。
)。
(3)设P点坐标为(﹣1,n),.
∵B(0,3),C(1,0),∴BC2=12+32=10。
分三种情况:
①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,
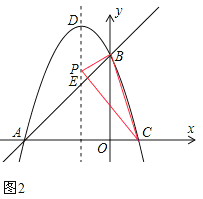
即(0+1)2+(n﹣3)2+10=(1+1)2+(n﹣0)2,
化简整理得6n=16,解得n=![]() 。
。
∴P点坐标为(﹣1,![]() )。
)。
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣![]() =
=![]() 。
。
∵点P的速度为每秒1个单位长度,∴t1=![]() 秒。
秒。
②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,
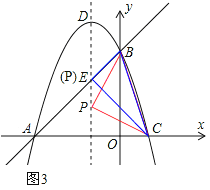
即(0+1)2+(n﹣3)2+(1+1)2+(n﹣0)2=10,
化简整理得n2﹣3n+2=0,解得n=2或1。
∴P点坐标为(﹣1,2)或(﹣1,1),
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣2=2或PD=4﹣1=3。
∵点P的速度为每秒1个单位长度,∴t2=2秒,t3=3秒。
③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,
即10+(1+1)2+(n﹣0)2=(0+1)2+(n﹣3)2,
化简整理得6n=﹣4,解得n=![]() 。
。
∴P点坐标为(﹣1,![]() )。
)。
∵顶点D的坐标为(﹣1,4),∴PD=4+![]() =
=![]() 。
。
∵点P的速度为每秒1个单位长度,
∴t4=![]() 秒。
秒。
综上所述,当t为![]() 秒或2秒或3秒或
秒或2秒或3秒或![]() 秒时,以P、B、C为顶点的三角形是直角三角形。
秒时,以P、B、C为顶点的三角形是直角三角形。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
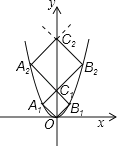
【题目】如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
解:OM=ON,证明如下:
连接CO,则CO是AB边上中线,
∵CA=CB,∴CO是∠ACB的角平分线.(依据1)
∵OM⊥AC,ON⊥BC,∴OM=ON.(依据2)
反思交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
拓展延伸:
(3)将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断线段OM、ON的数量关系与位置关系,并写出证明过程.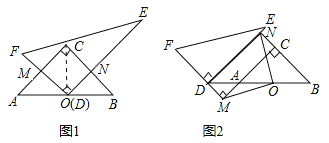
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便广大游客到昆明参观游览,铁道部门临时增开了一列南宁——昆明的直达快车,已知南宁、昆明两站的路程为828千米,一列普通快车与一列直达快车都由南宁开往昆明,直达快车的平均速度是普通快车平均速度的1.5倍,直达快车比普通快车后出发2小时,而先于普通快车4小时到达昆明,分别求出两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC,点D为BC中点.∠MDN=900,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论
①(BE+CF)=![]() BC,②
BC,②![]() ,③
,③![]() AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,问△AOB与△COD是否相似?有一位同学解答下:

∵AD∥BC,
∴∠ADO=∠CBO,∠DAO=∠BCO.
∴△AOD∽△BOC.
∴ ![]() .
.
又∵∠AOB=∠DOC,
∴△AOB∽△COD.
请判断这位同学的解答是否正确并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com