

分析 根据阴影部分的面积等于单位1减去空白部分的面积即可.
解答 解:第1次分割,把正方形的面积二等分,其中阴影部分的面积为$\frac{1}{2}$;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为$\frac{1}{2}$+$\frac{1}{{2}^{2}}$=$\frac{3}{4}$;
第3次分割,把上次分割图中空白部分的面积继续二等分,阴影部分面积之和$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$=$\frac{7}{8}$…;
…
第n次分割,所有阴影部分的面积之和1-$\frac{1}{{2}^{n}}$,最后空白部分的面积是$\frac{1}{{2}^{n}}$.
根据第n次分割图可得等式:$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+$\frac{1}{2^n}$=1-$\frac{1}{{2}^{n}}$.
故答案为:$\frac{1}{2}$,$\frac{1}{2}$+$\frac{1}{{2}^{2}}$=$\frac{3}{4}$,$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$=$\frac{7}{8}$,1-$\frac{1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$,1-$\frac{1}{{2}^{n}}$.
点评 本题考查了图形的变化类问题,解题的关键能够发现应用部分的面积的求法,难度不大.


科目:初中数学 来源: 题型:解答题
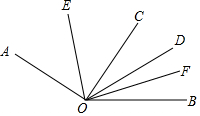 如图,已知∠AOB内部有顺次的四条射线:OE、OC、OD、OF、OE平分∠AOC,OF平分∠DOB
如图,已知∠AOB内部有顺次的四条射线:OE、OC、OD、OF、OE平分∠AOC,OF平分∠DOB查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com