
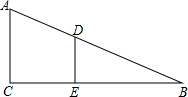
 身高1.5m的某同学沿平直路线匀速行走,路灯在行进路线的正上方某一高度,某时刻人影的长度为0.6m,前进4m后,影长变为1.4m,求路灯的高度.(提示:如图所示的两直角三角形ACB、DEB的边长之间存在如下关系:$\frac{AC}{DE}$=$\frac{BC}{BE}$)
身高1.5m的某同学沿平直路线匀速行走,路灯在行进路线的正上方某一高度,某时刻人影的长度为0.6m,前进4m后,影长变为1.4m,求路灯的高度.(提示:如图所示的两直角三角形ACB、DEB的边长之间存在如下关系:$\frac{AC}{DE}$=$\frac{BC}{BE}$) 分析 根据在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似解答即可.
解答  解:依题意得:DE=D′E=1.5m,EB=0.6m,EE′=4m,E′B′=1.4m.
解:依题意得:DE=D′E=1.5m,EB=0.6m,EE′=4m,E′B′=1.4m.
∵DE∥D′E∥AB,
∴可以得到△DBE∽△ABC,△AB′C∽△D′B′E′,
∴$\frac{DE}{AC}$=$\frac{BE}{BC}$,$\frac{D′E′}{AC}$=$\frac{B′E′}{B′C}$,
又∵DE=D′E,
∴$\frac{BE}{BC}$=$\frac{B′E′}{B′C}$,
∴$\frac{0.6}{CE+0.6}$=$\frac{1.4}{CE+4+1.4}$,
解得CE=3.
∴$\frac{1.5}{AC}$=$\frac{0.6}{3+0.6}$,
则AC=9.
答:路灯的高度是9m.
点评 本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某水产公司建了一个水池,用来临时存放活鱼,中间用两块隔板将水池分隔成甲、乙、丙三个水池,每块隔板在距离底面50厘米处都开一个方孔,且甲、丙的底面积相同,乙的底面积是甲的4倍,一次在清理水池后,甲池有10厘米深的水,现用两支水枪A,B,以相同的速度,同时分别向乙、丙水池注水,1分钟后,丙池水深40厘米.则甲、乙两池水深相差5厘米时所用的时间是( )
某水产公司建了一个水池,用来临时存放活鱼,中间用两块隔板将水池分隔成甲、乙、丙三个水池,每块隔板在距离底面50厘米处都开一个方孔,且甲、丙的底面积相同,乙的底面积是甲的4倍,一次在清理水池后,甲池有10厘米深的水,现用两支水枪A,B,以相同的速度,同时分别向乙、丙水池注水,1分钟后,丙池水深40厘米.则甲、乙两池水深相差5厘米时所用的时间是( )| A. | 0.5分钟 | B. | 1.5分钟 | ||
| C. | 0.5分钟或$\frac{11}{8}$分钟 | D. | 0.5分钟或$\frac{11}{8}$分钟或$\frac{59}{16}$分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
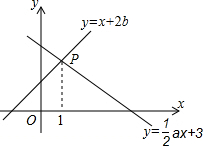 如图,已知函数y=x+2b和y=$\frac{1}{2}$ax+3的图象交于点P,则不等式x+2b>$\frac{1}{2}$ax+3的解集为x>1.
如图,已知函数y=x+2b和y=$\frac{1}{2}$ax+3的图象交于点P,则不等式x+2b>$\frac{1}{2}$ax+3的解集为x>1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com