
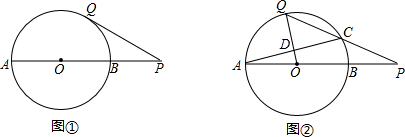
分析 (1)如图①,连接OQ.利用切线的性质和勾股定理来求PQ的长度.
(2)如图②,连接BC.利用三角形中位线的判定与性质得到BC∥OQ.根据圆周角定理推知BC⊥AC,所以,OQ⊥AC.
(3)利用割线定理来求PQ的长度即可.
解答 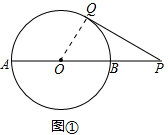 解:(1)如图①,连接OQ.
解:(1)如图①,连接OQ.
∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,
∴OQ⊥OP.
又∵BP=OB=OQ=2,
∴PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,即PQ=2$\sqrt{3}$;
(2)OQ⊥AC.理由如下: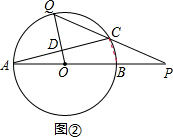 如图②,连接BC.
如图②,连接BC.
∵BP=OB,
∴点B是OP的中点,
又∵PC=CQ,
∴点C是PQ的中点,
∴BC是△PQO的中位线,
∴BC∥OQ.
又∵AB是直径,
∴∠ACB=90°,即BC⊥AC,
∴OQ⊥AC.
(3)如图②,PC•PQ=PB•PA,即$\frac{1}{2}$PQ2=2×6,
解得PQ=2$\sqrt{6}$.
点评 本题考查了圆的综合题.掌握圆周角定理,三角形中位线定理,平行线的性质,熟练利用割线定理进行几何计算.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:选择题
| A. | (-8)-8=0 | B. | 3+$\sqrt{3}$=3$\sqrt{3}$ | C. | (-3b)2=9b2 | D. | a6÷a2=a3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,0) | B. | (-1,-2) | C. | (-1,2) | D. | (3,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
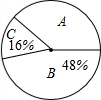 某班数学老师想了解学生对数学的喜欢程度,对全班50名学生进行调查,根据调查结果绘制了扇形统计图(如图所示),其中A表示“很喜欢”,B表示“一般”,C表示“不喜欢”,则该班“很喜欢”数学的学生有18人.
某班数学老师想了解学生对数学的喜欢程度,对全班50名学生进行调查,根据调查结果绘制了扇形统计图(如图所示),其中A表示“很喜欢”,B表示“一般”,C表示“不喜欢”,则该班“很喜欢”数学的学生有18人.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在白色方格地面上的概率是$\frac{3}{4}$.
一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在白色方格地面上的概率是$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 组别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 炉烟气排放 | 15% |
| D | 其他(滥砍滥伐等) | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com