
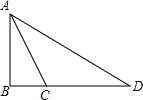
 如图,在△ABC中.∠B=90°,∠BAC=30°.AB=9cm,D是BC延长线上一点.且AC=DC.则
如图,在△ABC中.∠B=90°,∠BAC=30°.AB=9cm,D是BC延长线上一点.且AC=DC.则 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
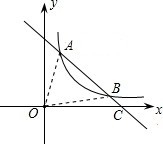 如图,双曲线y=
如图,双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
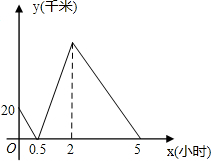 在一条笔直的航道上有A、B、C三个港口,一艘轮船从A港出发,匀速航行到C港后返回到B港,轮船离B港的距离y(千米),与航行时间x(小时)之间的函数关系如图所示,若航行过程中水流速度和轮船的静水速度保持不变,则水流速度为
在一条笔直的航道上有A、B、C三个港口,一艘轮船从A港出发,匀速航行到C港后返回到B港,轮船离B港的距离y(千米),与航行时间x(小时)之间的函数关系如图所示,若航行过程中水流速度和轮船的静水速度保持不变,则水流速度为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com