
【题目】在△ABC中,AB=4,AC=3,BC=5,动点P从点C出发,沿着CB方向运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
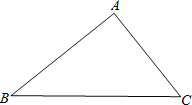
(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
【答案】(1)2.4;(2)t=1,![]() ,
,![]() .
.
【解析】
试题分析:(1)直接利用勾股定的逆定理得出△ABC是直角三角形,进而利用三角形面积得出答案;
(2)分别利用①当AP=AC时,②当AC=CP′时,③当AP″=CP″时,结合锐角三角函数关系得出答案.
解:(1)∵32+42=52,
∴△ABC是直角三角形,
设BC上的高为x,则![]() ×AB×AC=
×AB×AC=![]() ×BC×x,
×BC×x,
![]() =
=![]() x,
x,
解得:x=2.4,
故BC边上高为2.4;
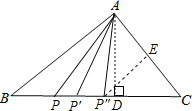
(2)①当AP=AC时,过A作AD⊥BC,
∵cosC=![]() =
=![]() ,
,
∴CD=ACcosC=3×![]() =
=![]() ,
,
∴CP=![]() ,
,
∵P的速度为每秒3个单位,
∴t=![]() ÷3=
÷3=![]() ;
;
②当AC=CP′时,
∵AC=3,
∴CP′=3,
∴t=3÷3=1;
③当AP″=CP″时,
过P″作P″E⊥AC,
∵AC=3,AP″=CP″,
∴EC=1.5,
∵cosC=![]() =
=![]()
CP″=![]() =
=![]() =2.5,
=2.5,
则t=2.5÷3=![]()
综上所述:t=1,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】已知下列实数:①﹣![]() ,②
,②![]() ,③3.14,④
,③3.14,④![]() ,⑤0,⑥﹣1.23,⑦
,⑤0,⑥﹣1.23,⑦![]() ,⑧1.232 232 223…(两个“3”之间依次多一个“2”),⑨﹣
,⑧1.232 232 223…(两个“3”之间依次多一个“2”),⑨﹣![]() .其中无理数有: ;整数有: ;负分数有: (只需填序号).
.其中无理数有: ;整数有: ;负分数有: (只需填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
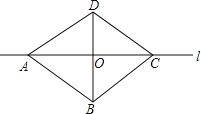
【题目】如图所示,直线l是四边形ABCD的对称轴,若AB=CD,有下面4个结论:
①AB∥CD;②AC⊥BD;③AO=CO;④AB⊥BC.
其中正确的结论有几个( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多边形的内角和是1440°,且这个多边形的每一个内角都相等,则这个多边形的一个外角是( )
A. 60° B. 45° C. 36° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P的坐标为(0,2),直线y=![]() 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )

A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com