
【题目】如图(1)△ABC中,H是高AD和BE的交点,且AD=BD.
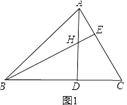
(1)请你猜想BH和AC的关系,并说明理由;
(2)若将图(1)中的∠A改成钝角,请你在图(2)中画出该题的图形,此时(1)中的结论还成立吗?(不必证明).

科目:初中数学 来源: 题型:
【题目】正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
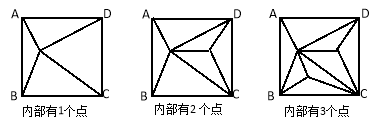
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
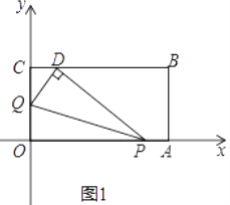
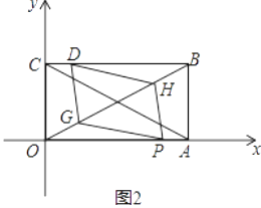
(1)求点B的坐标,并用含t的代数式表示OP,OQ;
(2)当t=1时,如图1,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D的坐标;
(3)在(2)的条件下,矩形对角线AC,BO交于M,取OM中点G,BM中点H,求证:当t=1时四边形DGPH是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了取得扶贫工作的胜利,某市对扶贫工作人员进行了扶贫知识的培训与测试,随机抽取了部分人员的测试成绩作为样本,并将成绩划分为![]() 四个不同的等级,绘制成不完整统计图如下图,请根据图中的信息,解答下列问题;
四个不同的等级,绘制成不完整统计图如下图,请根据图中的信息,解答下列问题;
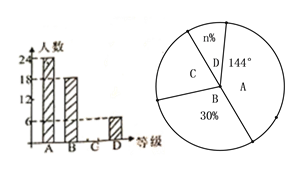
(1)求样本容量;
(2)补全条形图,并填空: ![]() ;
;
(3)若全市有5000人参加了本次测试,估计本次测试成绩为![]() 级的人数为多少?
级的人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,点E在CD上,点F在AB上,连接AE、CF、DF、BE,∠DAE=∠BCF.
(1)如图1,求证:四边形DFBE是平行四边形;
(2)如图2,若E是CD的中点,连接GH,在不添加任何辅助线的情况下,请直接写出图2中以GH为边或以GH为对角线的所有平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本![]() (单位:元)、销售价
(单位:元)、销售价![]() (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.
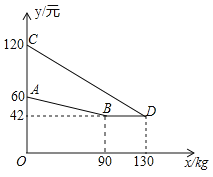
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com