
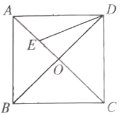
【题目】如图,正方形ABCD的对角线AC,BD交于点O,DE平分![]() 交OA于点E,若
交OA于点E,若![]() ,则线段OE的长为________.
,则线段OE的长为________.
【答案】2-![]()
【解析】
由正方形的性质可得AB=CD,∠COD=90°,OC=OD,∠ADB=∠ACD=∠CDO=45°,又因DE平分∠ODA,所以∠BDE=∠ADE=22.5°;在△ADE中,根据三角形的内角和定理可得∠CED=67.5°,所以∠CED=∠CDE=67.5°;根据等腰三角形的性质可得CD=CE=2;在等腰Rt△COD中,根据勾股定理求得OC=![]() ,由此即可求得OE的长.
,由此即可求得OE的长.
∵四边形ABCD为正方形,
∴AB=CD,∠COD=90°,OC=OD,∠ADB=∠ACD=∠CDO=45°,
∵DE平分![]() ,
,
∴∠BDE=∠ADE=22.5°,
∴∠CDE=∠BDE+∠CDO =67.5°;
在△ADE中,根据三角形的内角和定理可得∠CED=67.5°,
∴∠CED=∠CDE=67.5°,
∴CD=CE=2,
在等腰Rt△COD中,根据勾股定理求得OC=![]() ,
,
∴OE=CE-OC=2-![]() .
.
故答案为:2-![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,![]() ,
,![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要绕行
地需要绕行![]() 地,若打通穿山隧道,建成
地,若打通穿山隧道,建成![]() ,
,![]() 两地的直达高铁,可以缩短从
两地的直达高铁,可以缩短从![]() 地到
地到![]() 地的路程.已知:
地的路程.已知:![]() ,
,![]() ,
,![]() 公里,求隧道打通后与打通前相比,从
公里,求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程将约缩短多少公里?(参考数据:
地的路程将约缩短多少公里?(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为![]() 米,广场的长为
米,广场的长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示花坛的面积和广场空地的面积;
(2)若休闲广场的长为500米,宽为200米,圆形花坛的半径为20米,求广场空地的面积;(计算结果保留![]() ;
;
(3)在(2)的情况下,若![]() 取3.14,求休闲广场的绿化率是多少?
取3.14,求休闲广场的绿化率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知含字母a,b的代数式是:3[a2+2(b2+ab﹣2)]﹣3(a2+2b2)﹣4(ab﹣a﹣1)
(1)化简代数式;
(2)小红取a,b互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0,那么小红所取的字母b的值等于多少?
(3)聪明的小刚从化简的代数式中发现,只要字母b取一个固定的数,无论字母a取何数,代数式的值恒为一个不变的数,那么小刚所取的字母b的值是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)△ABC中,H是高AD和BE的交点,且AD=BD.
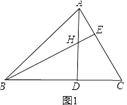
(1)请你猜想BH和AC的关系,并说明理由;
(2)若将图(1)中的∠A改成钝角,请你在图(2)中画出该题的图形,此时(1)中的结论还成立吗?(不必证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点p第2019次碰到矩形的边时点P的坐标为( )
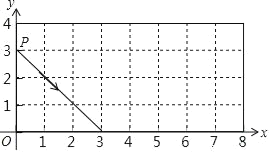
A. ( 1,4 )B. ( 5,0 )C. ( 8,3 )D. ( 6,4 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蔬菜公司采购了若干吨的某种蔬菜,计划加工之后销售,若单独进行粗加工,需要20天才能完成;若单独进行精加工,需要30天才能完成,已知每天单独粗加工比单独精加工多生产10吨.
(1)求公司采购了多少吨这种蔬菜?
(2)据统计,这种蔬菜经粗加工销售,每吨利润2000元;经精加工后销售,每吨利润涨至2500元.受季节条件限制,公司必须在24天内全部加工完毕,由于两种加工方式不能同时进行,公司为尽可能多获利,安排将部分蔬菜进行精加工后,其余蔬菜进行粗加工,并恰好24天完成,加工的这批蔬菜若全部售出,求公司共获得多少元的利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com