
����Ŀ����һ����ֽƬOABC����ƽ��ֱ������ϵ�У�O��0��0����A��6��0����C��0��3��������Q�ӵ�O������ÿ��1����λ�����ٶ���OC���յ�C�˶����˶�![]() ��ʱ������P�ӵ�A��������ȵ��ٶ���AO���յ�O�˶���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������P���˶�ʱ��Ϊt���룩��
��ʱ������P�ӵ�A��������ȵ��ٶ���AO���յ�O�˶���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������P���˶�ʱ��Ϊt���룩��
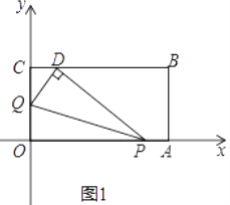
��1�����B�����꣬���ú�t�Ĵ���ʽ��ʾOP��OQ��
��2����t=1ʱ����ͼ1������OPQ��PQ���ۣ���Oǡ������CB���ϵĵ�D�������D�����ꣻ
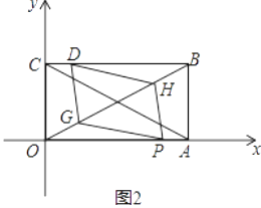
��3���ڣ�2���������£����ζԽ���AC��BO����M��ȡOM�е�G��BM�е�H����֤����t=1ʱ�ı���DGPH��ƽ���ı��Σ�
���𰸡���1��B��6��3����OQ=![]() +t�� OP= 6��t����2��D��1��3������3��֤��������.
+t�� OP= 6��t����2��D��1��3������3��֤��������.
��������
���⣨1�����ݾ��ε����������B�����꣬���ݶ����������OP��OQ�ij��ȣ���2�������۵�ͼ�ε��������OQ��DQ�ij��ȣ�Ȼ����ݹ��ɶ������CD�ij��ȣ��õ���D�����ꣻ��3������һ��Ա�ƽ������ȵ��ı���Ϊƽ���ı��ν����ж���
�����������1��B��6,3����OP="OA-AP=6-t," OQ=![]() +t��
+t��
��2����t=1ʱ��OP=5��OQ=![]() ,��CQ=3-
,��CQ=3-![]() =
=![]() ��
��
���۵���֪����OPQ�ա�DPQ,
��OQ=DQ=![]()
�ɹ��ɶ���,�ã�CD=1
��D��1,3��
��3�����ı���OABC�Ǿ��Σ�
��OA=BC,
����CD=AP=1��
��BC-CD=OA-AP,��BD=OP,
��OM=MB,GΪOM�е㣬HΪBM�е� ,
��OG="BH,"
��OA��BC
���1=��2
����POG����DBH��OG=BH����1=��2��OP=DB
���POG�ա�DBH
���OGP=��BHD��PG=DH
���MGP=��DHM
��PG��DH
����PG=DH
���ı���DGPH��ƽ���ı��Σ�


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֪ʶ��
�����dz�����ѧ��һ����Ҫ���ߣ�����������Խ������������ؽ��.�о��������Ƿ�����������Ҫ�Ĺ��ɣ��������ϵ�![]() ����
����![]() ��ʾ�����ֱ�Ϊ
��ʾ�����ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ����֮��ľ���
����֮��ľ���![]() ���߶�
���߶�![]() ���е��ʾ����Ϊ
���е��ʾ����Ϊ![]() .
.
�������龳��
��ͼ�������ϵ�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() ��ʾ����Ϊ8����
��ʾ����Ϊ8����![]() �ӵ�
�ӵ�![]() ��������ÿ��3����λ���ȵ��ٶ����������������˶���ͬʱ��
��������ÿ��3����λ���ȵ��ٶ����������������˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ��������ÿ��2����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊ
��������ÿ��2����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊ![]() �루
�루![]() ��.
��.
���ۺ����ã�
��1����գ�
��![]() ��
��![]() ����֮��ľ���
����֮��ľ���![]() ________���߶�
________���߶�![]() ���е��ʾ����Ϊ__________.
���е��ʾ����Ϊ__________.
���ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() ���
���![]() ��ʾ����Ϊ____________����
��ʾ����Ϊ____________����![]() ��ʾ����Ϊ___________.
��ʾ����Ϊ___________.
�۵�![]() _________ʱ��
_________ʱ��![]() ��
��![]() ��������������������ʾ����Ϊ__________.
��������������������ʾ����Ϊ__________.
��2����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() .
.
��3������![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() ���˶������У��߶�
���˶������У��߶�![]() �ij����Ƿ����仯�����仯����˵�����ɣ������䣬������߶�
�ij����Ƿ����仯�����仯����˵�����ɣ������䣬������߶�![]() �ij�.
�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����������й㳡���ĽǶ����һ��뾶��ͬ���ķ�֮һԲ�εĻ�̳����Բ�εİ뾶Ϊ![]() �ף��㳡�ij�Ϊ
�ף��㳡�ij�Ϊ![]() �ף���Ϊ
�ף���Ϊ![]() �ף�
�ף�
��1������ʽ��ʾ��̳������㳡�յص������
��2�������й㳡�ij�Ϊ500�ף���Ϊ200�ף�Բ�λ�̳�İ뾶Ϊ20�ף���㳡�յص������������������![]() ��
��
��3���ڣ�2��������£���![]() ȡ3.14�������й㳡���̻����Ƕ��٣�
ȡ3.14�������й㳡���̻����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ĸa��b�Ĵ���ʽ�ǣ�3[a2+2��b2+ab��2��]��3��a2+2b2����4��ab��a��1��
��1���������ʽ��
��2��С��ȡa��b��Ϊ������һ����ֵ���뻯��Ĵ���ʽ�У�ǡ�ü���ô���ʽ��ֵ����0����ôС����ȡ����ĸb��ֵ���ڶ��٣�
��3��������С�մӻ���Ĵ���ʽ�з��֣�ֻҪ��ĸbȡһ���̶�������������ĸaȡ����������ʽ��ֵ��Ϊһ�������������ôС����ȡ����ĸb��ֵ�Ƕ����أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����ABC�У�H�Ǹ�AD��BE�Ľ��㣬��AD=BD��
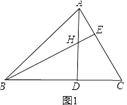
��1���������BH��AC�Ĺ�ϵ����˵��������
��2������ͼ��1���еġ�A�ijɶ۽ǣ�������ͼ��2���л��������ͼ�Σ���ʱ��1���еĽ��ۻ������𣿣�����֤������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�ֱ�Ϊ�����ϵ����㣬A���Ӧ����Ϊ��20��B���Ӧ����Ϊ100��
![]()
��1����д����A��B���������ȵĵ�M����Ӧ������ ����
��2������һֻ��������P��B����������6��λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�A���������4��λ/����ٶ������˶���x�����ֻ���������������ϵ�C�����������з������x����ָ����C��ʾ������
��3��������������P��B�����ʱ����6��λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�A���������4��λ/����ٶ�Ҳ�����˶���y�����ֻ���������������ϵ�D�����������з������y��ָ����D��ʾ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�ӣ�0��3������������ʾ�ķ����˶���ÿ���������εı�ʱ����������ʱ����ǵ�������ǣ�����p��2019���������εı�ʱ��P������Ϊ��������
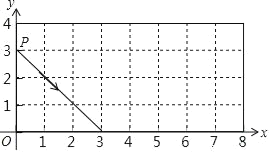
A. �� 1��4 ��B. �� 5��0 ��C. �� 8��3 ��D. �� 6��4 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���A��![]() ����������һ�����㣬��P�Ǻ���
����������һ�����㣬��P�Ǻ���![]() ��
��![]() ��0����һ�����㣬PB��
��0����һ�����㣬PB��![]() ���ڵ�B������PA,����P�ĺ�����������ʱ���ı���OAPB��������ᣨ�� ��
���ڵ�B������PA,����P�ĺ�����������ʱ���ı���OAPB��������ᣨ�� ��
A. ������ B. ������� C. ��С D. �ȼ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
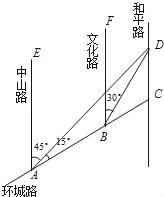
����Ŀ����ͼ��AC��ij�л���·��һ�Σ�AE��BF��CD�����ϱ�����Ľֵ������뻷��·AC�Ľ���·�ڷֱ���A��B��C����������������Dλ�ڵ�A�ı�ƫ��45������B�ı�ƫ��30�������ϣ�AB=2km����DAC=15�㣮
��1����B��D֮��ľ��룻
��2����C��D֮��ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com