
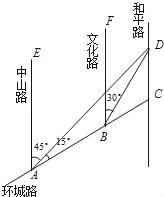
【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
(1)求点B的坐标,并用含t的代数式表示OP,OQ;
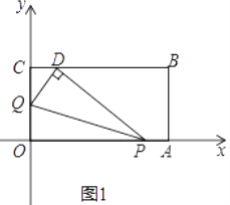
(2)当t=1时,如图1,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D的坐标;
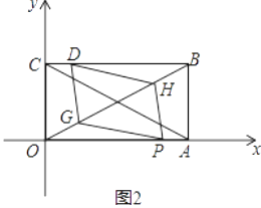
(3)在(2)的条件下,矩形对角线AC,BO交于M,取OM中点G,BM中点H,求证:当t=1时四边形DGPH是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
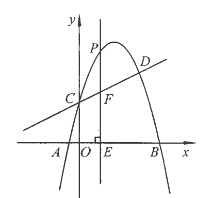
【题目】如图,抛物线![]() 与直线
与直线![]() 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为![]() 。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由;
(3)若存在点P,使∠PCF=450,请直接写出相应的点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,求证∠1=∠2.以下是推理过程,请你填空:
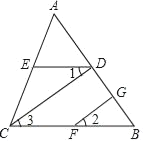
解:∵CD⊥AB,FG⊥AB
∴∠CDB=∠FGB=90°( 垂直定义)
∴ ∥FG( )
∴ =∠3 ( )
又∵DE∥BC ( 已知 )
∴∠ =∠3 ( 两直线平行,内错角相等 )
∴∠1=∠2 ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本![]() (单位:元)、销售价
(单位:元)、销售价![]() (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.
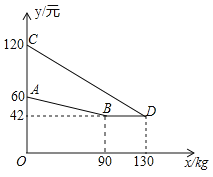
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业个人旅游年消费情况进行问卷调查,随机抽查部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成尚不完整的表和图(如图).
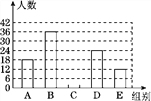
组别 | 个人年消费金额x/元 | 频数(人数) | 频率 |
A | x≤2 000 | 18 | 0.15 |
B | 2 000<x≤4 000 | a | b |
C | 4 000<x≤6 000 | ||
D | 6 000<x≤8 000 | 24 | 0.20 |
E | x>8 000 | 12 | 0.10 |
合计 | c | 1.00 |
根据以上信息回答下列问题:
(1)a=________,b=________,c=________,并将条形统计图补充完整;
(2)在这次调查中,个人年消费金额的中位数出现在________组;
(3)若这个企业有3 000名员工,请你估计个人旅游年消费金额在6 000元以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以![]() 个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以
个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以![]() 个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
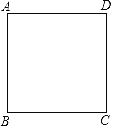
A. 点AB. 点BC. 点CD. 点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() ,
,![]() ,
,![]() .在此运动过程中,下列结论:①
.在此运动过程中,下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积保持不变;④当
的面积保持不变;④当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
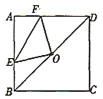
A.①②B.②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com