
【题目】如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以![]() 个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以
个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以![]() 个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
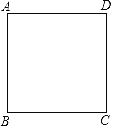
A. 点AB. 点BC. 点CD. 点D
【答案】D
【解析】
设两只电子蚂蚁每隔x秒相遇一次,根据正方形周长=二者速度之和×时间,可得出关于x的一元一次方程,解之即可得出两只电子蚂蚁每隔2秒相遇一次,再结合电子蚂蚁Q的速度、出发点及运动方向可得出它们第1次、第2次、第3次、第4次、第5次……相遇点,结合2019÷4=504……3可得出结论.
解:设两只电子蚂蚁每隔x秒相遇一次,
根据题意得:(![]() +
+![]() )x=1×4,
)x=1×4,
解得:x=2.
∵电子蚂蚁Q从点A出发,以![]() 个单位长度/秒的速度绕正方形作逆时针运动,
个单位长度/秒的速度绕正方形作逆时针运动,
∴它们第1次相遇在B点,第2次相遇在C点,第3次相遇在D点,第4次相遇在A点,第5次相遇在B点,第6次相遇在C点,….
又∵2019÷4=504……3,
∴第2019次相遇和第3次相遇地点相同,即第2019次相遇在点D.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点p第2019次碰到矩形的边时点P的坐标为( )
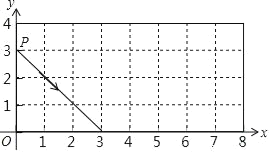
A. ( 1,4 )B. ( 5,0 )C. ( 8,3 )D. ( 6,4 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蔬菜公司采购了若干吨的某种蔬菜,计划加工之后销售,若单独进行粗加工,需要20天才能完成;若单独进行精加工,需要30天才能完成,已知每天单独粗加工比单独精加工多生产10吨.
(1)求公司采购了多少吨这种蔬菜?
(2)据统计,这种蔬菜经粗加工销售,每吨利润2000元;经精加工后销售,每吨利润涨至2500元.受季节条件限制,公司必须在24天内全部加工完毕,由于两种加工方式不能同时进行,公司为尽可能多获利,安排将部分蔬菜进行精加工后,其余蔬菜进行粗加工,并恰好24天完成,加工的这批蔬菜若全部售出,求公司共获得多少元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
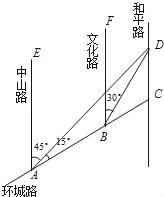
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EB交AC于M,交FC于D,AB交FC于N,∠E=∠F=90,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN。其中正确的结论有( )
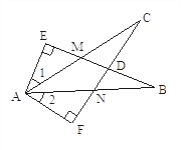
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(2,0),B ( 2,0),C为 y 轴负半轴上一点,D是第四象限内一动点,且始终有BDA 2ACO 成立,过C 点作CE BD 于点 E .
(1)求证:DAC DBC ;
(2)若点 F 在 AD 的延长线上,求证:CD 平分BDF ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 经过
经过![]() 顶点
顶点![]() 的一条直线,
的一条直线,![]() .
.![]() 分别是直线
分别是直线![]() 上两点,且
上两点,且![]() .
.
(1)若直线![]() 经过
经过![]() 的内部,且
的内部,且![]() 在射线
在射线![]() 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若![]() ,
,![]() ,
,
则![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如图2,若![]() ,请添加一个关于
,请添加一个关于![]() 与
与![]() 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线![]() 经过
经过![]() 的外部,
的外部,![]() ,请提出
,请提出![]() 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com