
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
【答案】(1)![]() 或
或![]() (2)
(2)![]() 或
或![]() (3)
(3)![]() .
.
【解析】
(1)利用平方差公式进行因式分解;
(2)利用提公因式法对不等式的左边进行因式分解,再求解可得;
(3)需要分类讨论:①![]() ,②
,②![]() ,据此求解可得.
,据此求解可得.
解:(1)由原不等式得:(x+3)(x-3)>0
∴![]() 或
或![]()
解得 x>3或x<-3.
故答案为:![]() 或
或![]() ;
;
(2)∵![]() ,
,
∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:
①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]() ,
,
∴![]() 的解集为
的解集为![]() 或
或![]() ,
,
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() ;
;
(3)由有理数的乘法法则:两数相乘,异号得负,得:
①![]() ②
②![]()
解不等式组①,得![]() ,
,
解不等式组②,不等式组无解,
∴不等式![]() 的解集为
的解集为![]() .
.
故答案为:(1)![]() 或
或![]() (2)
(2)![]() 或
或![]() (3)
(3)![]() .
.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( )

A. ac<0 B. a+b+c<0 C. b2﹣4ac<0 D. b=8a
查看答案和解析>>
科目:初中数学 来源: 题型:
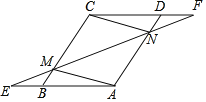
【题目】已知,如图,在ABCD中,延长AB到点E,延长CD到点F,使得BE=DF,连接EF,分别交BC,AD于点M,N,连接AM,CN.
(1)求证:△BEM≌△DFN;
(2)求证:四边形AMCN是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
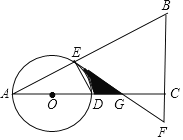
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园里有一人设了个游戏摊位,游客只需掷一枚正方体骰子,如果出现3点,就可获得价值10元的奖品,每抛掷1次骰子只需付1元的费用.小明在摊位前观察了很久,记下了游客的中奖情况:
游客 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
抛掷次数 | 30 | 20 | 25 | 6 | 16 | 50 | 12 |
中奖次数 | 1 | 0 | 0 | 1 | 0 | 2 | 0 |
看了小明的记录,你有什么看法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
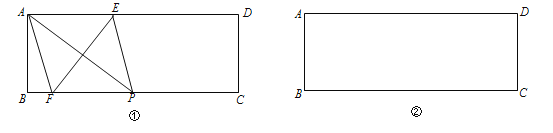
【题目】如图,在矩形ABCD中,AB=1,BC=3.
(1)在图①中,P是BC上一点,EF垂直平分AP,分别交AD、BC边于点E、F,求证:四边形AFPE是菱形;
(2)在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD的边上,并直接标出菱形的边长.(保留作图痕迹,不写作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com