
【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.

【答案】BB′=![]() .
.
【解析】先利用旋转的旋转得CA=CA′,CB=CB′,∠ACA′=∠BCB′=60°,则可判断△ACA′和△BCB′均为等边三角形,所以BB′=BC,∠A=60°,∠CBB′=60°,再利用∠A=60°得∠ABC=30°,所以BC=![]() CA=
CA=![]() ,从而得到BB′的长.
,从而得到BB′的长.
解:∵将△ABC绕点C顺时针旋转60°至△A′B′C,
∴CA=CA′,CB=CB′,∠ACA′=∠BCB′=60°,
∴△ACA′和△BCB′均为等边三角形,
∴BB′=BC,∠A=60°,∠CBB′=60°,
∵点A′在AB上,∠ACB=90°,
∴∠A=60°,∠ABC=90°﹣∠A=30°,
在Rt△ABC中,BC=![]() CA=
CA=![]() ,
,
∴BB′=![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.

(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG 的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点E在边AB上,点F是边BC上不与点B、C重合的一个动点,把
,点E在边AB上,点F是边BC上不与点B、C重合的一个动点,把![]() 沿EF折叠,点B落在点
沿EF折叠,点B落在点![]() 处.若
处.若![]() ,当
,当![]() 是以
是以![]() 为腰的等腰三角形时,线段
为腰的等腰三角形时,线段![]() 的长为__________.
的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
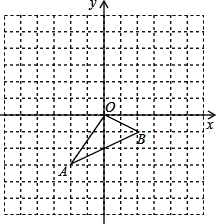
【题目】如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3).
(1)求三角形ABO的面积;
(2)作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′ 、B′ ;
(3)P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形.
(2)当α=150°时,试判断△AOD的形状(按角分类),并说明理由.
(3)求∠OAD的度数.
(4)探究:当α= 时,△AOD是等腰三角形.(不必说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上,过点C作直线![]() ,点D在点C的左边。
,点D在点C的左边。
(1)若BD平分∠ABC,![]() ,则
,则![]() _____°;
_____°;
(2)如图②,若![]() ,作∠CBA的平分线交OC于E,交AC于F,试说明
,作∠CBA的平分线交OC于E,交AC于F,试说明![]() ;
;
(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H.在点B运动过程中![]() 的值是否变化?若不变,求出其值;若变化,求出变化范围.
的值是否变化?若不变,求出其值;若变化,求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
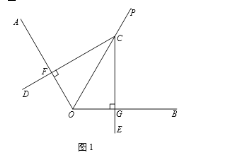
【题目】已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.
(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;
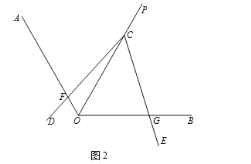
(2)如图2,若∠AOB=120,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)求x和y的值;
(2)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com