
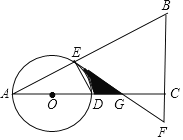
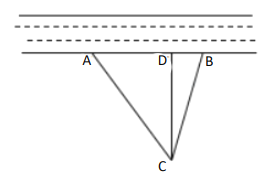
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
【答案】(1)EF是⊙O的切线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接OE,根据等腰三角形的性质得到∠A=∠AEO,∠B=∠BEF,于是得到∠OEG=90°,即可得到结论;(2)由AD是⊙O的直径,得到∠AED=90°,根据三角形的内角和得到∠EOD=60°,求得∠EGO=30°,根据三角形和扇形的面积公式即可得到结论.
试题解析:(1)连接OE,
∵OA=OE,∴∠A=∠AEO,
∵BF=EF,∴∠B=∠BEF,
∵∠ACB=90°,∴∠A+∠B=90°,∴∠AEO+∠BEF=90°,
∴∠OEG=90°,∴EF是⊙O的切线;
(2)∵AD是⊙O的直径,∴∠AED=90°,
∵∠A=30°,∴∠EOD=60°,∴∠EGO=30°,
∵AO=2,∴OE=2,∴EG=2![]() ,
,
∴阴影部分的面积=![]() =
= ![]() .
.



 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,画出函数y=2x+4的图象;

(1)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(2)在(1)的条件下,求出△AOB的面积;
(3)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)
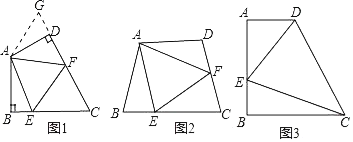
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E、F分别是边BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是:延长FD到点G,使GD=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 .
(探索延伸)
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
(学以致用)
如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是边AB上一点,当∠DCE=45°,BE=2时,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的信息,解答下列问题:

(1)放入一个小球水面升高 ,![]() ,放入一个大球水面升高
,放入一个大球水面升高 ![]() ;
;
(2)如果要使水面上升到50![]() ,应放入大球、小球各多少个?
,应放入大球、小球各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
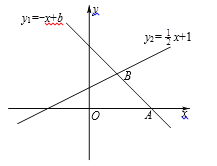
【题目】如图,已知一次函数y1=-x+b的图象交x轴于点A(3,0),与一次函数y2=![]() x+1的图象交于点B,
x+1的图象交于点B,
(1)求一次函数y1=-x+b的表达式;
(2)当x取哪些值时,0<y1<y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
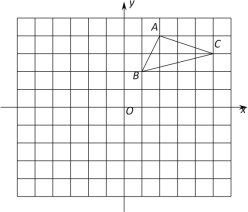
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)AB的长等于 ;
(2)画出△ABC向下平移5个单位后得到△A1B1C1,并写出此时点A1的坐标;
(3)画出△ABC绕原点O旋转180后得到的△A2B2C2,并写出此时点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.
(1)求甲、乙两种品牌的足球的单价各是多少元?
(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄![]() ,河边原有两个取水点
,河边原有两个取水点![]() ,其中
,其中![]() ,由于某种原因,由
,由于某种原因,由![]() 到
到![]() 的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点
的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点![]() 在同一条直线上),并新修一条路
在同一条直线上),并新修一条路![]() ,测得
,测得![]() 千米,
千米,![]() 千米,
千米,![]() 千米.
千米.
(1)问![]() 是否为从村庄
是否为从村庄![]() 到河边最近的路?请通过计算加以说明:
到河边最近的路?请通过计算加以说明:
(2)求原来的路线![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com