
【题目】(问题背景)
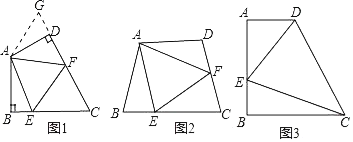
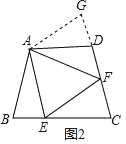
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E、F分别是边BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是:延长FD到点G,使GD=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 .
(探索延伸)
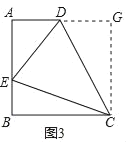
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
(学以致用)
如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是边AB上一点,当∠DCE=45°,BE=2时,则DE的长为 .
【答案】【问题背景】:EF=BE+FD;【探索延伸】:结论EF=BE+DF仍然成立,见解析;【学以致用】:5.
【解析】
[问题背景]延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
[探索延伸]延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
[学以致用]过点C作CG⊥AD交AD的延长线于点G,利用勾股定理求得DE的长.
[问题背景】解:如图1,
在△ABE和△ADG中,
∵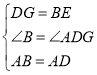 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵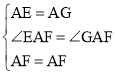 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+FD,
∴EF=BE+FD;
故答案为:EF=BE+FD.
[探索延伸]解:结论EF=BE+DF仍然成立;
理由:如图2,延长FD到点G.使DG=BE.连结AG,
在△ABE和△ADG中,
∵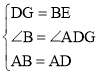 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵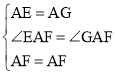 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+FD,
∴EF=BE+FD;
[学以致用]如图3,过点C作CG⊥AD,交AD的延长线于点G,
由【探索延伸】和题设知:DE=DG+BE,
设DG=x,则AD=6﹣x,DE=x+3,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴(6﹣x)2+32=(x+3)2,
解得x=2.
∴DE=2+3=5.
故答案是:5.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】某市从不同学校随机抽取100名初中生对“使用数学教辅用书的册数”进行调查,统计结果如下:
册数 | 0 | 1 | 2 | 3 |
人数 | 10 | 20 | 30 | 40 |
关于这组数据,下列说法正确的是( )
A.众数是2册B.中位数是2册
C.平均数是3册D.方差是1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( )

A. ac<0 B. a+b+c<0 C. b2﹣4ac<0 D. b=8a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;

(2)有公共顶点的![]() 条射线可以组成_____个小于平角的角;
条射线可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
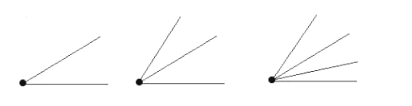
(3)你学过的知识里还有满足类似规律的吗?试看写一个.
查看答案和解析>>
科目:初中数学 来源: 题型:
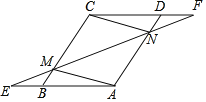
【题目】已知,如图,在ABCD中,延长AB到点E,延长CD到点F,使得BE=DF,连接EF,分别交BC,AD于点M,N,连接AM,CN.
(1)求证:△BEM≌△DFN;
(2)求证:四边形AMCN是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
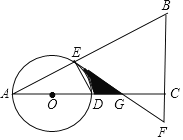
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有![]() 个选项,第二道单选题有
个选项,第二道单选题有![]() 个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(![]() )如果小明第一题不使用“求助”,那么小明答对第一道题的概率是__________.
)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是__________.
(![]() )如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明通关的概率.
)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明通关的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com