练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

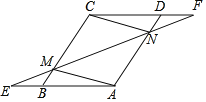
    【题目】已知，如图，在ABCD中，延长AB到点E，延长CD到点F，使得BE=DF，连接EF，分别交BC，AD于点M，N，连接AM，CN．

    （1）求证：△BEM≌△DFN；

    （2）求证：四边形AMCN是平行四边形．

    【答案】（1）证明见解析；（2）证明见解析

    【解析】

    （1）根据平行四边形的性质得出∠BAD=∠BCD，AB∥CD，根据平行线的性质得出∠BAD=∠ADF，∠EBC=∠BCD，∠E=∠F，求出∠ADF=∠EBC，根据全等三角形的判定得出即可；

    （2）根据全等求出DN=BM，求出AN=CM，根据平行四边形的判定得出即可．

    解：（1）∵四边形ABCD是平行四边形，

    ∴∠BAD=∠BCD，AB∥CD，

    ∴∠BAD=∠ADF，∠EBC=∠BCD，∠E=∠F，

    ∴∠ADF=∠EBC，

    在△DFN和△BEM中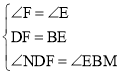

    ∴△DFN≌△BEM（ASA）；

    （2）四边形ANCM是平行四边形，理由是：

    ∵由（1）知△DFN≌△BEM，

    ∴DN=BM，

    ∵四边形ABCD是平行四边形，

    ∴AD=BC，且AD∥BC，

    ∴AD﹣DN=BC﹣BM，

    ∴AN=CM，AN∥CM，

    ∴四边形ANCM是平行四边形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,直线AB和直线BC相交于点B,连接AC,点D. E. H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°，

    (1)求证：∠CEF=∠EAD；

    (2)若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小丽购买学习用品的收据如表，因污损导致部分数据无法识别，根据下表，解决下列问题:

    (1)小丽买了自动铅笔、记号笔各几支?

    (2)若小丽再次购买软皮笔记本和自动铅笔两种文具，共花费15元，则有哪几种不同的购买方案?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题背景）

    如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，点E、F分别是边BC、CD上的点，且∠EAF＝60°，试探究图中线段BE、EF、FD之间的数量关系．

    小王同学探究此问题的方法是：延长FD到点G，使GD＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是　 　．

    （探索延伸）

    如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E、F分别是边BC、CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由．

    （学以致用）

    如图3，在四边形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC＝6，E是边AB上一点，当∠DCE＝45°，BE＝2时，则DE的长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

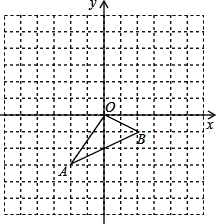
    【题目】如图，三角形ABO中，A（﹣2，﹣3）、B（2，﹣1），三角形A′B′O′是三角形ABO平移之后得到的图形，并且O的对应点O′的坐标为（4，3）.

    （1）求三角形ABO的面积;

    （2）作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′　　　、B′　　　；

    （3）P（x，y）为三角形ABO中任意一点，则平移后对应点P′的坐标为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据图中给出的信息，解答下列问题：

    （1）放入一个小球水面升高 ，，放入一个大球水面升高 ；

    （2）如果要使水面上升到50，应放入大球、小球各多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读理解下面的例题，再按要求解答下列问题：

    例题：解一元二次不等式.

    解∵，∴可化为.

    由有理数的乘法法则：两数相乘，同号得正，得：①②

    解不等式组①，得，解不等式组②，得

    ∴的解集为或.

    即一元二次不等式的解集为或.

    （1）一元二次不等式的解集为____________；

    （2）试解一元二次不等式；

    （3）试解不等式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为(2，4)．

    （1）AB的长等于 ；

    （2）画出△ABC向下平移5个单位后得到△A1B1C1，并写出此时点A1的坐标；

    （3）画出△ABC绕原点O旋转180后得到的△A2B2C2，并写出此时点C2的坐标．

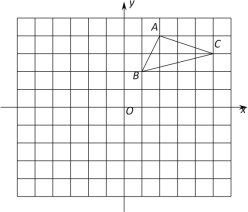
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知直线AB∥CD．

    （1）如图1，直接写出∠ABE，∠CDE和∠BED之间的数量关系是　 　．

    （2）如图2，BF，DF分别平分∠ABE，∠CDE，那么∠BFD和∠BED有怎样的数量关系？请说明理由．

    （3）如图3，点E在直线BD的右侧，BF，DF仍平分∠ABE，∠CDE，请直接写出∠BFD和∠BED的数量关系　 　．

    查看答案和解析>>

    同步练习册答案