
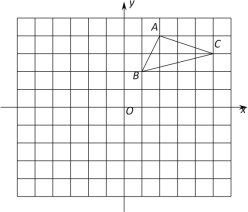
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)AB的长等于 ;
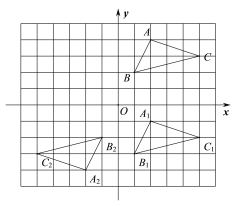
(2)画出△ABC向下平移5个单位后得到△A1B1C1,并写出此时点A1的坐标;
(3)画出△ABC绕原点O旋转180后得到的△A2B2C2,并写出此时点C2的坐标.
【答案】(1)![]() ;(2)见解析,(2,-1);(3)见解析,(-5,-3)
;(2)见解析,(2,-1);(3)见解析,(-5,-3)
【解析】
(1) 根据△ABC的三个顶点都在格点上,点A的坐标为(2,4),得到网格每一个的长度,再用勾股定理即可得到答案
(2)直接用平移的定义即可画图,再根据向下平移横坐标不变纵坐标变小即可得到答案;
(3)根据旋转的定义即可画出图形,再根据旋转后的点与原来的点关于原点对称即可得到答案
解:(1)∵△ABC的三个顶点都在格点上,点A的坐标为(2,4),
∴网格的每一格长度为1,,
∴![]() (勾股定理);
(勾股定理);
(2)图中△A1B1C1即为所求,
∵△ABC向下平移5个单位后得到△A1B1C1,
∴A点横坐标不变,纵坐标减少了5,
∴此时点A1的坐标为(2,-1);
(3)图中△A2B2C2即为所求,
∵△ABC绕原点O旋转180后得到的△A2B2C2,
∴点C2的坐标与点C的坐标关于原点对称,
∵C点坐标从直角坐标系可以直接得到为:(5,3)
此时点C2的坐标为(-5,-3);


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
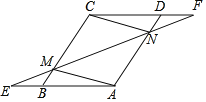
【题目】已知,如图,在ABCD中,延长AB到点E,延长CD到点F,使得BE=DF,连接EF,分别交BC,AD于点M,N,连接AM,CN.
(1)求证:△BEM≌△DFN;
(2)求证:四边形AMCN是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
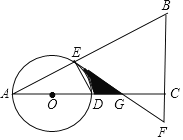
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园里有一人设了个游戏摊位,游客只需掷一枚正方体骰子,如果出现3点,就可获得价值10元的奖品,每抛掷1次骰子只需付1元的费用.小明在摊位前观察了很久,记下了游客的中奖情况:
游客 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
抛掷次数 | 30 | 20 | 25 | 6 | 16 | 50 | 12 |
中奖次数 | 1 | 0 | 0 | 1 | 0 | 2 | 0 |
看了小明的记录,你有什么看法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有![]() 个选项,第二道单选题有
个选项,第二道单选题有![]() 个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(![]() )如果小明第一题不使用“求助”,那么小明答对第一道题的概率是__________.
)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是__________.
(![]() )如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明通关的概率.
)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来购物的不同支付方式走进校园,某数学兴趣小组就此进行了抽样调查调查结果显示,支付方式有:A、微信,B、支付宝,C、现金,D、其他.该小组对学校超市一天内购买者的支付方式进行调查统计,得到如图所示的两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题.

(1)求出这次抽样调查的样本容量
(2)请补全条形统计图,并求出在扇形统计图中A种支付方式所对应的圆心角的度数
(3)若该校约有1200名学生在小超市购物,请你估计使用A和B两种支付方式的学生共有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com