练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】公园里有一人设了个游戏摊位，游客只需掷一枚正方体骰子，如果出现3点，就可获得价值10元的奖品，每抛掷1次骰子只需付1元的费用．小明在摊位前观察了很久，记下了游客的中奖情况：

    游客

    1

    2

    3

    4

    5

    6

    7

    抛掷次数

    30

    20

    25

    6

    16

    50

    12

    中奖次数

    1

    0

    0

    1

    0

    2

    0

    看了小明的记录，你有什么看法？

    【答案】见解析.

    【解析】试题分析：先根据正方体骰子的特点计算出3出现的概率，再与小明实际记录的中奖次数相比较即可得出结论．

    试题解析：解：对于一个普通的正方体骰子，3点出现的概率应为．

    小明记录的抛掷次数为159次，中奖的次数应为27次左右，而实际中奖次数只有4次，于是可以怀疑摆摊人所用的骰子质量分布不均匀，要进一步证实这种怀疑，可以通过更多的试验来完成．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】问题背景：我们学习了整式的乘法，两个多项式相乘，我们可以运用法则，将其展开，例如：，而将等号的左右两边互换，我们得到了，等号的左边是一个多项式，而右边是几个整式相乘的形式，我们规定将一个多项式写成几个整式相乘的形式，这种运算称之为“因式分解”

    问题提出：

    如何将进行因式分解呢？

    问题探究：

    数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题.初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释

    例如：我们可以通过表示几何图形面积的方法来快速的对多项式进行因式分解.

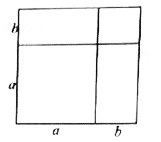
    如图所示边长为的大正方形是由1个边长为的正方形，2个边长为的长方形，1个边长为的正方形，组成，我们可以用两种方法表示大正方形的面积，这个图形的面积可以表示成：或

    ∴

    我们将等号左边的多项式写成了右边两个整式相乘的形式，从而成功的对多项式进行了因式分解

    请你类比上述方法，利用图形的几何意义对多项式进行因式分解（要求自己构图并写出推证过程）

    问题拓展：

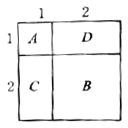
    如何利用图形几何意义的方法推导：？如图，表示1个的正方形，即，表示1个的正方形，与恰好可以拼成1个的正方形，因此：、、就可以表示2个的正方形，即，而、、、恰好可以拼成一个的大正方形.由此可得：

    尝试解决：

    请你类比上述推导过程，利用图形几何意义方法推导出的值.

    （要求自己构造图形并写出推证过程）.

    解：

    归纳猜想：_________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

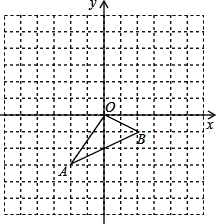
    【题目】如图，三角形ABO中，A（﹣2，﹣3）、B（2，﹣1），三角形A′B′O′是三角形ABO平移之后得到的图形，并且O的对应点O′的坐标为（4，3）.

    （1）求三角形ABO的面积;

    （2）作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′　　　、B′　　　；

    （3）P（x，y）为三角形ABO中任意一点，则平移后对应点P′的坐标为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读理解下面的例题，再按要求解答下列问题：

    例题：解一元二次不等式.

    解∵，∴可化为.

    由有理数的乘法法则：两数相乘，同号得正，得：①②

    解不等式组①，得，解不等式组②，得

    ∴的解集为或.

    即一元二次不等式的解集为或.

    （1）一元二次不等式的解集为____________；

    （2）试解一元二次不等式；

    （3）试解不等式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】己知：如图①，直线MN⊥直线PQ，垂足为O，点A在射线OP上，点B在射线OQ上（A、B不与O点重合），点C在射线ON上，过点C作直线，点D在点C的左边。

    （1）若BD平分∠ABC，，则_____°；

    （2）如图②，若，作∠CBA的平分线交OC于E，交AC于F，试说明；

    （3）如图③，若∠ADC=∠DAC，点B在射线OQ上运动，∠ACB的平分线交DA的延长线于点H.在点B运动过程中的值是否变化？若不变，求出其值；若变化，求出变化范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

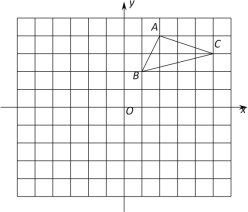
    【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为(2，4)．

    （1）AB的长等于 ；

    （2）画出△ABC向下平移5个单位后得到△A1B1C1，并写出此时点A1的坐标；

    （3）画出△ABC绕原点O旋转180后得到的△A2B2C2，并写出此时点C2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

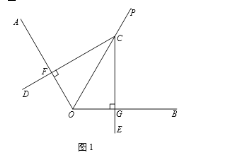
    【题目】已知OP平分∠AOB，∠DCE的顶点C在射线OP上，射线CD交射线OA于点F，射线CE交射线OB于点G．

    （1）如图1，若CD⊥OA，CE⊥OB，请直接写出线段CF与CG的数量关系；

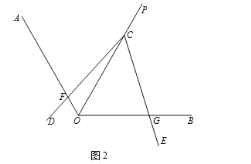
    （2）如图2，若∠AOB=120，∠DCE=∠AOC，试判断线段CF与CG的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小华是花店的一名花艺师，她每天都要为花店制作普通花束和精致花束，她每月工作20天，每天工作8小时，她的工资由基本工资和提成工资两部分构成，每月的基本工资为l800元，另每制作一束普通花束可提2元，每制作一束精致花束可提5元．她制作两种花束的数量与所用时间的关系见下表：

    制作普通花束（束）

    制作精致花束（束）

    所用时间（分钟）

    10

    25

    600

    15

    30

    750

    请根据以上信息，解答下列问题：

    （1）小华每制作一束普通花束和每制作一束精致花束分别需要多少分钟？

    （2）2019年11月花店老板要求小华本月制作普通花束的总时间不少于3000分钟且不超过5000分钟，则小华该月收入最多是多少元？此时小华本月制作普通花束和制作精致花束分别是多少束？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，过正方形ABCD顶点B，C的⊙O与AD相切于点P，与AB，CD分别相交于点E，F，连接EF．

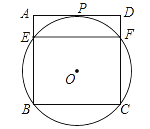
    （1）求证：PF平分∠BFD；

    （2）若tan∠FBC= ，DF=，求EF的长．

    查看答案和解析>>

    同步练习册答案