
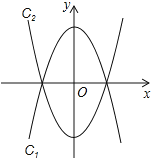
【题目】将抛物线c1: ![]() 沿x轴翻折,得到抛物线c2,如图1所示.
沿x轴翻折,得到抛物线c2,如图1所示.
(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与![]() 轴的交点从左到右依次为D、E.
轴的交点从左到右依次为D、E.
①当B、D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
【答案】(1)![]() (2)①2,1/2,②是矩形,m=1
(2)①2,1/2,②是矩形,m=1
【解析】试题分析:因为二次函数的图像关于x轴对称时,函数中的a,c,互为相反数,b值不变,函数向左平移时,纵坐标不变,横坐标均减少平移个单位,可假定成立,由直角三角形性质得到验证。解:(1)抛物线c2的表达式是![]() ; 2分;
; 2分;

(2)①点A的坐标是(![]() ,0), 3分;
,0), 3分;
点E的坐标是(![]() ,0). 4分;
,0). 4分;
②假设在平移过程中,存在以点A,M,E为顶点的三角形是直角三角形.
由题意得只能是![]() .
.
过点M作MG⊥x轴于点G.
由平移得:
点M的坐标是(![]() ,
, ![]() ), 5分;
), 5分;
∴点G的坐标是(![]() ,0),
,0),
∴![]() ,
, ![]() ,
,
![]() ,
,
在Rt△AGM中,
∵ tan![]() ,
,
∴![]() , 6分;
, 6分;
∵![]() ,
,
∴![]() ,
,
∴tan![]() ,
,
∴![]() , 7分;
, 7分;
∴![]() . 8分.
. 8分.
所以在平移过程中,当![]() 时,存在以点A,M,E为顶点的三角形是直角三角形.
时,存在以点A,M,E为顶点的三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,三角形A1B1C1是由三角形ABC平移后得到的,已知三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0-6,y0-2).
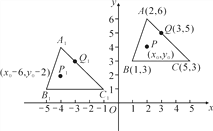
(1)已知A(2,6),B(1,3),C(5,3),Q(3,5),请写出A1,B1,C1,Q1的坐标;
(2)试说明三角形A1B1C1是如何由三角形ABC得到的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a=(﹣0.1)0 , b=(﹣0.1)﹣1 , c=(﹣ ![]() )﹣2 , 那么a,b,c的大小关系为( )
)﹣2 , 那么a,b,c的大小关系为( )
A.a>b>c
B.c>a>b
C.c>b>a
D.a>c>b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列二次函数中,顶点坐标为(-5,0),且开口方向、形状与y=-x2的图象相同的是( )
A.y=(x-5)2B.y=x2-5C.y=-(x+5)2D.y=(x+5)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小明将一张长为4、宽为3的矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用点F表示).
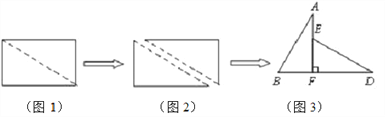
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
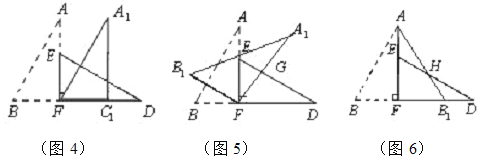
(1)将图3中的△ABF沿BD向右平移到图4中![]() 的位置,其中点B与点F 重合,请你求出平移的距离 ;
的位置,其中点B与点F 重合,请你求出平移的距离 ;
(2)在图5中若∠GFD=60°,则图3中的△ABF绕点 按 方向旋转 到图5的位置;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,试问:△AEH和△HB1D的面积大小关系.说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com