
����Ŀ����ͼ,��ƽ��ֱ������ϵ�У���ABC��ֱ��������,��ACB=90,AC=BC,OA=1��OC=4��������y=![]() +bx+c����A��B���㣬�����ߵĶ���ΪD��
+bx+c����A��B���㣬�����ߵĶ���ΪD��
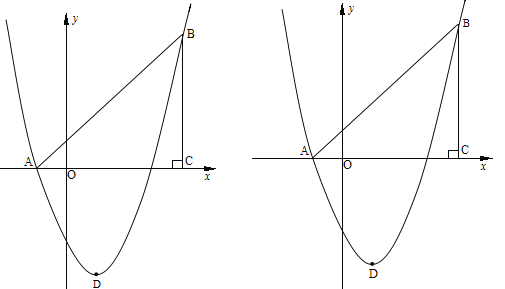
(1)����b,c��ֵ��
(2)����E��ֱ��������ABCб��AB��һ����(��A��B����)������E��x��Ĵ��߽��������ڵ�F�����߶�EF�ij������ʱ�����E�����ꣻ
(3)���ڣ�2���������£������Ե�E��B��F��DΪ������ı��ε�������������������Ƿ����һ��P��ʹ��EFP����EFΪֱ�DZߵ�ֱ��������? �����ڣ�������е�P�����ꣻ�������ڣ�˵������.
���𰸡�(1)��b=��2��c=��3��(2)����![]() ��
��![]() ����(3)��
����(3)��![]() ��
��![]() ��
��![]()
![]() ��
��![]()
��������
���������(1)���������������A����B�����꣬Ȼ��������ʽ���b��c��ֵ��(2)���������ֱ��AB�Ľ���ʽ�������E��F�����꣬���EF�ij��ȣ�Ȼ����ݺ��������������ֵ��(3)�����������D�͵�F�����꣬���ı��ε����ת������BEF����DEF������⣻����E��a��EF�����������P�������P�����꣬������̣���F��b��EF�����������P�������P�����꣬�������.
�����������1������֪�ã�A��-1��0�� B��4��5�������κ���y=![]() +bx+c��ͼ����A��-1��0��B(4,5)
+bx+c��ͼ����A��-1��0��B(4,5)
��![]() ��ã�b=-2 c=-3
��ã�b=-2 c=-3
(2)����ͼ����ֱ��AB������A��-1��0�� B(4,5) ��ֱ��AB�Ľ���ʽΪ��y=x+1
�������y=![]() ��2x��3 �����E(t��t+1),��F��t��
��2x��3 �����E(t��t+1),��F��t��![]() ��2t��3��
��2t��3��
��EF=(t+1)��(![]() ��2t��3)=
��2t��3)=![]()
����![]() ʱ��EF�����ֵ=
ʱ��EF�����ֵ=![]() ����E������Ϊ��
����E��������![]() ��
��![]() ��
��
����ͼ��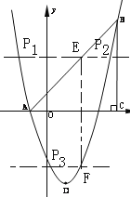
˳�����ӵ�E��B��F��D���ı���EBFD��
�������F�����꣨![]() ��
��![]() ��,��D��������1��-4��
��,��D��������1��-4��
S![]() =S
=S![]() +S
+S![]()
=![]() =
=![]() /p>
/p>
����ͼ����)����E��a��EF���������ڵ�P,���P(m,![]() )���У�
)����![]() ���:
���:![]() ,
,![]() ��
��![]() ,
, ![]()
��������F��b��EF����������![]() ����
����![]() ��n��
��n��![]() ������
������![]()
��ã�![]() ��
��![]() �����F�غϣ���ȥ����
�����F�غϣ���ȥ����![]()
![]()
�������������е�P�����꣺![]() ��
��![]()
![]() ��
��![]() ��ʹ��EFP�����EFΪֱ�DZߵ�ֱ�������Σ�
��ʹ��EFP�����EFΪֱ�DZߵ�ֱ�������Σ�


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���ABC=90�㣬��ABC���ܳ�Ϊ17cm��б��������BD��Ϊ ![]() ����������ε����Ϊ ��
����������ε����Ϊ �� 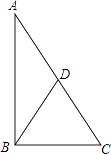
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�۵���ʹ��Aǡ���������εĶԳ�����O�����ۺ�ΪEF��������ABCD�ı߳�Ϊ2cm����A=120�㣬��EF=cm�� 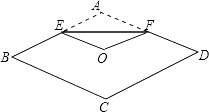
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�칫¥AB�ĺ�����һ������CD�������������ļн���22��ʱ���칫¥�ڽ������ǽ�����¸�3��Ӱ��CE���������������н���45��ʱ���칫¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��27�ľ��루B��F��C��һ��ֱ���ϣ���
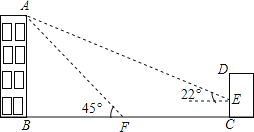
��1����칫¥AB�ĸ߶ȣ�
��2����Ҫ��A��E֮���һЩ���죬�������A��E֮��ľ��룮
���ο����ݣ�sin22����![]() ��cos22����
��cos22����![]() ��tan22����
��tan22����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��2��x��1��2+3�Ķ��������ǣ� ��
A.����1��3��
B.��1��3��
C.��1����3��
D.����1����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ����8ʱ�ϵ�һ�ڿΣ�45���Ӻ��¿Σ���ڿ��з���ת���ĽǶ�Ϊ�� ��
A.45��
B.90��
C.180��
D.270��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�۵���ʹ��D���B�غϣ���C���ڵ�C�䴦���ۺ�ΪEF������ABE=20�㣬��ô��EFC��Ķ���Ϊ�ȣ� 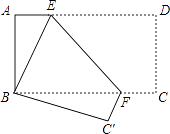
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��2��a��1������2a��3��+3
��2��2��x2y+3xy2����3��2xy2��4x2y��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com