
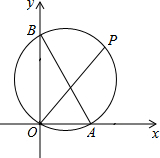 如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为
如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为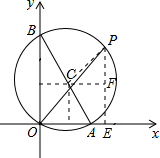 解:∵OB=4,OA=2,
解:∵OB=4,OA=2,| OA2+OB2 |
| 5 |
| 5 |
| 5 |
| 5 |


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
 如图,△ABC在平面直角坐标系,点A(0,3
如图,△ABC在平面直角坐标系,点A(0,3| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
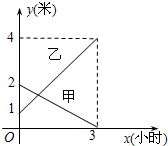 自来水公司有甲、乙两个长方体的蓄水池,现将甲池中的水以每小时8m3的速度注入乙池,则两水池中水的高度y(m)与注水的时间x(h)之间的函数图象如图所示.若要乙池的蓄水量是甲池的2倍,则注水的时间应为( )
自来水公司有甲、乙两个长方体的蓄水池,现将甲池中的水以每小时8m3的速度注入乙池,则两水池中水的高度y(m)与注水的时间x(h)之间的函数图象如图所示.若要乙池的蓄水量是甲池的2倍,则注水的时间应为( )| A、2h | ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com