
 如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$.
如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$. 分析 如图作GM⊥AB于M,连接FG、AG,设AE=EF=x,在RT△BEF中利用勾股定理求出AE,设DG=y,利用AG=GF,列出方程求出DG,在RT△EGM中即可解决问题.
解答 解:如图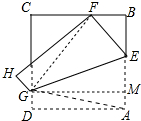 作GM⊥AB于M,连接FG、AG.
作GM⊥AB于M,连接FG、AG.
∵四边形EGHF是由四边形EGDA翻折得到,
∴EF=EA,GF=AG,
设EF=AE=x,在RT△EFB中,∵EF2=BF2+BE2,
∴x2=22+(5-x)2,
∴x=$\frac{29}{10}$,
∴AE=EF=$\frac{29}{10}$,
设DG=y,则y2+52=(5-y)2+32,
∴y=$\frac{9}{10}$,
∵∠D=∠DAB=∠AMG=90°,
∴四边形DAMG是矩形,
∴AM=DG=$\frac{9}{10}$,EM=AE-AM=2,GM=AD=5,
∴tan∠AEG=$\frac{GM}{EM}$=$\frac{5}{2}$.
故答案为$\frac{5}{2}$.
点评 本题考查翻折变换、勾股定理等知识,添加辅助线构造直角三角形是解决问题的关键,学会利用勾股定理列出方程,用方程的思想解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 15000名学生的总体 | B. | 每个学生是个体 | ||
| C. | 500名学生是所抽取的一个样本 | D. | 样本容量是500 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
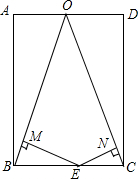 如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB、OC,点E在线段BC上(点E不与点B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为( )
如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB、OC,点E在线段BC上(点E不与点B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为( )| A. | 6 | B. | 1.5 | C. | $\frac{3}{10}\sqrt{10}$ | D. | $\frac{3}{5}\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
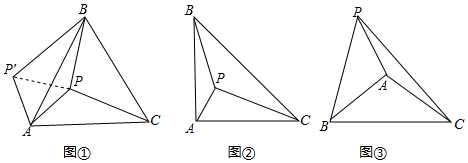
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
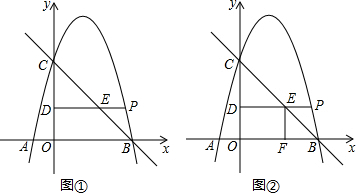
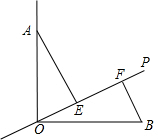 如图,∠AOB=90°,OA=OB,OP是∠AOB内可以绕着点O自由转动的一条射线,分别过点A、B作AE⊥OP、BF⊥OP,垂足分别为点E、F,假设OP从OB出发,绕着点O逆时针转动到OA(OP不与OB、OA重合),转动的角度为α.
如图,∠AOB=90°,OA=OB,OP是∠AOB内可以绕着点O自由转动的一条射线,分别过点A、B作AE⊥OP、BF⊥OP,垂足分别为点E、F,假设OP从OB出发,绕着点O逆时针转动到OA(OP不与OB、OA重合),转动的角度为α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com