
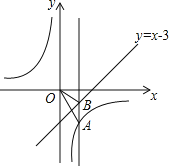
【题目】如图,已知点A、P在反比例函数y=![]() (k<0)的图象上,点B、Q在直线y=x-3的图象上,点B的纵坐标为-1,AB⊥x轴,且S△OAB=4,若P、Q两点关于y轴对称,设点P的坐标为(m,n).
(k<0)的图象上,点B、Q在直线y=x-3的图象上,点B的纵坐标为-1,AB⊥x轴,且S△OAB=4,若P、Q两点关于y轴对称,设点P的坐标为(m,n).
(1)求点A的坐标和k的值;
(2)求![]() 的值.
的值.
【答案】(1)(2,-5);k=-10;(2)![]()
【解析】
(1)先由点B在直线y=x-3的图象上,点B的纵坐标为-1,将y=-1代入y=x-3,求出x=2,即B(2,-1).由AB⊥x轴可设点A的坐标为(2,t),利用S△OAB=4列出方程![]() (-1-t)×2=4,求出t=-5,得到点A的坐标为(2,-5);将点A的坐标代入y=
(-1-t)×2=4,求出t=-5,得到点A的坐标为(2,-5);将点A的坐标代入y=![]() ,即可求出k的值;
,即可求出k的值;
(2)根据关于y轴对称的点的坐标特征得到Q(-m,n),由点P(m,n)在反比例函数y=-![]() 的图象上,点Q在直线y=x-3的图象上,得出mn=-10,m+n=-3,再将
的图象上,点Q在直线y=x-3的图象上,得出mn=-10,m+n=-3,再将![]() 变形为
变形为![]() ,代入数据计算即可.
,代入数据计算即可.
解:(1)∵点B在直线y=x-3的图象上,点B的纵坐标为-1,
∴当y=-1时,x-3=-1,解得x=2,
∴B(2,-1).
设点A的坐标为(2,t),则t<-1,AB=-1-t.
∵S△OAB=4,
∴![]() (-1-t)×2=4,
(-1-t)×2=4,
解得t=-5,
∴点A的坐标为(2,-5).
∵点A在反比例函数y=![]() (k<0)的图象上,
(k<0)的图象上,
∴-5=![]() ,解得k=-10;
,解得k=-10;
(2)∵P、Q两点关于y轴对称,点P的坐标为(m,n),
∴Q(-m,n),
∵点P在反比例函数y=-![]() 的图象上,点Q在直线y=x-3的图象上,
的图象上,点Q在直线y=x-3的图象上,
∴n=-![]() =-m-3,
=-m-3,
∴mn=-10,m+n=-3,
∴![]() =
=![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=2x+4的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,与x轴交于点C,且点B的横坐标为-3.
(k≠0)的图象交于A,B两点,与x轴交于点C,且点B的横坐标为-3.
(1)求反比例函数的解析式;
(2)连接AO,求△AOC的面积;
(3)在△AOC内(不含边界),整点(横纵坐标都为整数的点)共有______个.
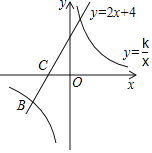
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠B1A1 C1=45°,∠B1=45°,且A1B1=CB.若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M,设AC=a.
(1)计算A1C1的长;
(2)当α=30°时,证明:B1C1∥AB;
(3)若a=![]() ,当α=45°时,计算两个三角板重叠部分图形的面积;
,当α=45°时,计算两个三角板重叠部分图形的面积;
(4)当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.
(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=2﹣
,tan15°=2﹣![]() ,sin75°=
,sin75°=![]() ,cos75°=
,cos75°=![]() ,tan75°=2+
,tan75°=2+![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下:
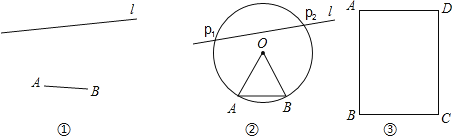
第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于P1,P2;所以图中P1,P2即为所求的点.
(1)在图②中,连接P1A,P1B,试说明∠AP1B=30°;
(方法迁移)
(2)已知矩形ABCD,如图③,BC=2![]() ,AB=m.
,AB=m.
①若P为AD边上的点,且满足∠BPC=60°的点P恰有1个,求m的值.
②当m=4时,若P为矩形ABCD外一点,且满足∠BPC=60°,求AP长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方.下列结论:①4a-2b+c=0;②a-b+c<0;③2a+c>0;④2a-b+1>0.其中正确结论的个数是( )个.
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 正方形ABCD与正五边形EFGHM的边长相等,初始如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合…按这样的方式将正方形依次绕点H、M、E旋转后,正方形中与EF重合的是( )

A. ABB. BCC. CDD. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 梯形ABCD中,AD∥BC,请用尺规作图并解决问题.
(1)作AB中点E,连接DE并延长交射线CB于点F,在DF的下方作∠FDG=∠ADE,边DG交BC于点G,连接EG;
(2)试判断EG与DF的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)请用列表法或树状图写出所有的等可能性结果,写出所有个位数字是6的“两位递增数”;
(2)求抽取的“两位递增数”的个位数字与十位数字之积能被5整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:基本不等式![]() ≤
≤![]() (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把![]() 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数,![]() 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() 即是x+
即是x+![]() ≥2
≥2![]()
∴x+![]() ≥2
≥2
当且仅当x=![]() 即x=1时,x+
即x=1时,x+![]() 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+![]() ,当x为何值时,函数有最值,并求出其最值.
,当x为何值时,函数有最值,并求出其最值.
(2)当x>0时,式子x2+1+![]() ≥2成立吗?请说明理由.
≥2成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com