Question

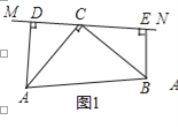
【题目】（10分）在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E，

证明：DE=AD+BE；

Answer 1

【答案】详见解析．

【解析】

试题分析：由∠ACB＝90°，得∠ACD+∠BCE=90°，而AD⊥MN于D，BE⊥MN于点E，则∠ADC=∠CEB=90°，根据等角的余角相等得到∠ACD=∠CBE，易得△ADC≌△CEB，所以AD=CE，DC=BE，即可得到DE=DC+CE=BE+AD．

试题解析：证明：∵∠ACB＝90°，

∴∠ACD+∠BCE=90°，

而AD⊥MN于D，BE⊥MN于点E，

∴∠ADC=∠CEB=90°，

∴∠ACD+∠BCE=90°∠BCE+∠CBE=90°，

∴∠ACD=∠CBE．

在△ADC和△CEB中，

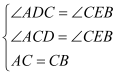
∴△ADC≌△CEB，

∴AD=CE，DC=BE，

∴DE=DC+CE=BE+AD；