
����Ŀ����1����ͼ�٣���Rt��ABC��Rt��DBE�У���ABC=��DBE=90����AB=BC=3��BD=BE=1������CD��AE��
��֤����BCD�ա�BAE��
��2���ڣ�1���������£���![]() ʱ���ӳ�CD��AE�ڵ�F����ͼ�ڣ���AF�ij���
ʱ���ӳ�CD��AE�ڵ�F����ͼ�ڣ���AF�ij���
��3���ڣ�2���������£��߶�BC���Ƿ����һ��P��ʹ����PBDΪ���������Σ������ڣ���ֱ��д��������PBDΪ����������ʱ���߶�PB�ij����������ڣ���˵������.
���𰸡���1��֤������������2��2![]() -1; (3) ����, 1��
-1; (3) ����, 1�� ![]() .
.
��������������(1)����ͬ�ǵ������ȿɵã���CBD=��ABE��������SAS���ɵó����.��2���ɡ�BCD�ա�BAE���õ���OAF=��OCB�����ݡ�8���͡�֤����AFO=��CBO=90�㣬��RT��BDC�����ù��ɶ������CD����֤��BD=EF���ɽ�����⣮��3����������۵ó�������̶������PB���ɽ�����⣮
���������
��1���ߡ�ABC=��DBE=90�㼴��CBD+��ABD=��ABD+��ABE=90��
���CBD=��ABE
�֡�AB=BC��DB=BE
���BCD�ա�BAE��SAS��
(2)����ͼ���У���AB��CF���ڵ�O��
�ɣ�1����֪����BCD�ա�BAE��
���OAF=��OCB��CD=AE��
�ߡ�AOF=��COB��
���AFO=��CBO=90����
��CF��AE��
��BD��AE��
��BD��CF��
��RT��CDB�У��ߡ�CDB=90����BC=3��BD=1��
��CD=AE=![]() ,
,
�ߡ�BDF=��DFE=��DBE=90����
���ı���EFDB�Ǿ��Σ�
��EF=BD=1��
��AF=AE-EF=2![]() -1.
-1.
��3������.
��PB=BD=1ʱ����PBDΪ���������Σ�PB=1��
��PD=BD=1ʱ����PBDΪ���������Σ�PB=![]()


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������˵���У���ȷ�ĸ����ǣ�������
����a+b=0����|a|=|b|
����a��0����|a|=��a
����|a|=|b|����a=b
����a����������a2=����a��2
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
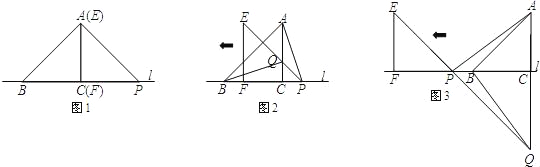
����Ŀ�����Ϊ45����ֱ�������ε���ֱ�DZ߳�Ҳ��ȣ������������γ�Ϊ����ֱ�������Σ����dz��õ����ǰ�����һ����������������Σ�Ҳ�ɳ���Ϊ����ֱ�����ǰ壮������ȫ�ȵĵ���ֱ�����ǰ尴��ͼ1���ã����б�BC��FP����ֱ��l�ϣ���EF���AC�غϣ�
��1������EFP��ֱ��l����ƽ�Ƶ�ͼ2��λ��ʱ��EP��AC�ڵ�Q������AP��BQ�����벢д��BQ��AP�������������ϵ��λ�ù�ϵ����֤����IJ��룻
��2������EFP��ֱ��l����ƽ�Ƶ�ͼ3��λ��ʱ��EP���ӳ��߽�AC���ӳ����ڵ�Q������AP��BQ������Ϊ��1�����������BQ��AP��������ϵ��λ�ù�ϵ��������������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
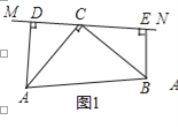
����Ŀ����10�֣�����ABC�У���ACB=90����AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E��
֤����DE=AD+BE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y����x��2��2+3�Ķ��������ǣ� ��
A.(2��3)B.(��2��3)C.(2����3)D.(��2����3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P�ǹ���x��5�ζ���ʽ��Q�ǹ���x��3�ζ���ʽ���� ( )
A. P��Q�ǹ���x��8�ζ���ʽ B. P��Q�ǹ���x�Ķ��ζ���ʽ
C. 2P��5Q�ǹ���x��8�ζ���ʽ D. 2P��5Q�ǹ���x����ζ���ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.  �ȱ�������
�ȱ�������
B. ![]() ƽ���ı���
ƽ���ı���
C. ![]() ������
������
D.  �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̻�һ�����ݲ�����С��ͳ�����ǣ� ��
A. ƽ���� B. ���� C. ���� D. ��λ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com