
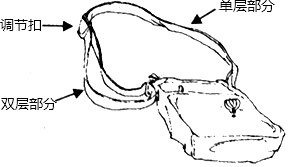
 如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:| 单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
| 双层部分的长度y(cm) | … | 73 | 72 | 71 | … |
分析 (1)观察表格可知,y是x的一次函数,设y=kx+b,利用待定系数法即可解决问题;
(2)列出方程组即可解决问题;
(3)由题意当y=0,x=150,当x=0时,y=75,可得75≤l≤150.
解答 解:(1)观察表格可知,y是x的一次函数,设y=kx+b,
则有$\left\{\begin{array}{l}{4k+b=73}\\{6k+b=72}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=75}\end{array}\right.$,
∴y=-$\frac{1}{2}$x+75.
(2)由题意$\left\{\begin{array}{l}{x+y=120}\\{y=-\frac{1}{2}x+75}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=90}\\{y=30}\end{array}\right.$,
∴单层部分的长度为90cm.
(3)由题意当y=0,x=150,当x=0时,y=75,
∴75≤l≤150.
点评 本题考查一次函数的应用、待定系数法等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 定义:有三个内角相等的四边形叫三等角四边形.
定义:有三个内角相等的四边形叫三等角四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 计算“$\frac{1}{2}$-1$\frac{3}{4}$”的按键顺序是 | |
| B. | 计算“3×105-28”的按键顺序是 | |
| C. | “已知SinA=0.3,求锐角A”的按键顺序是 | |
| D. | 计算“($\frac{1}{2}$)5”的按键顺序是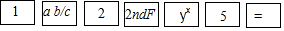 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24里 | B. | 12里 | C. | 6里 | D. | 3里 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
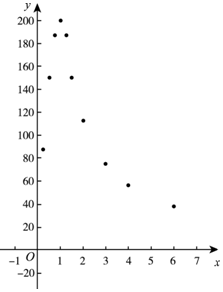 阅读下列材料:
阅读下列材料:| 饮酒后的时间x (小时) | … | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ | 1 | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | 6 | … |
| 血液中酒精含量y (毫克/百毫升) | … | $\frac{175}{2}$ | 150 | $\frac{375}{2}$ | 200 | $\frac{375}{2}$ | 150 | $\frac{225}{2}$ | $\frac{225}{3}$ | $\frac{225}{4}$ | 45 | $\frac{225}{6}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
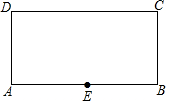 如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.
如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2m}{{3}^{n}}$ | B. | $\frac{{2}^{m}}{3n}$ | C. | $\frac{2m}{{n}^{3}}$ | D. | $\frac{{m}^{2}}{3n}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com