
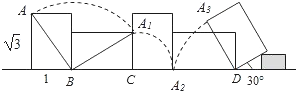
分析 由弧长、面积公式分别求出各段弧长、面积,相加即可求解.
解答 解:$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2
由题意可得,第一段弧长为$\widehat{A{A}_{1}}$=$\frac{1}{2}$π×2=πdm,面积=$\frac{1}{4}$π×22=πdm2;
第二段弧长$\widehat{{A}_{1}{A}_{2}}$为=$\frac{1}{2}$π×1=$\frac{1}{2}$πdm,面积=$\frac{1}{4}$π×12=$\frac{1}{4}$πdm2;
第三段弧长$\widehat{{A}_{2}{A}_{3}}$为=$\frac{1}{3}$π×$\sqrt{3}$=$\frac{\sqrt{3}}{3}$πdm,面积=$\frac{1}{6}$π×($\sqrt{3}$)2=$\frac{1}{2}$πdm2;
故点A走过的路程的长为$\frac{3}{2}$π+$\frac{\sqrt{3}}{3}$πdm,走过的弧度所在扇形的总面积为$\frac{7}{4}$πdm2.
点评 本题考查弧长、面积公式,求出各段弧长的半径和圆心角是解题的关键,有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
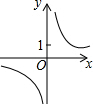 已知直线y=kx+1与双曲线y=$\frac{4}{x}$(如图所示).
已知直线y=kx+1与双曲线y=$\frac{4}{x}$(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
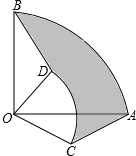 把两个圆心角都是90°的扇形OAB与扇形OCD按如图所示位置叠放在一起,连接AC,BD.
把两个圆心角都是90°的扇形OAB与扇形OCD按如图所示位置叠放在一起,连接AC,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
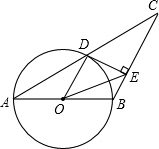 如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,并过点D作⊙O的切线交BC于点E,若CD=10,CE=8.
如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,并过点D作⊙O的切线交BC于点E,若CD=10,CE=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{9}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com