
 古希腊人用石子在沙滩上摆成各种形状来研究,如,一,五,十二,二十二…为五边形,则8个五边形是多少?
古希腊人用石子在沙滩上摆成各种形状来研究,如,一,五,十二,二十二…为五边形,则8个五边形是多少? 分析 根据第1个五边形是:1=$\frac{3}{2}$×02+$\frac{5}{2}$×0+1,第2个五边形是:5=$\frac{3}{2}$×12+$\frac{5}{2}$×1+1,第3个五边形是:12=$\frac{3}{2}$×22+$\frac{5}{2}$×2+1,第4个五边形是:22=$\frac{3}{2}$×32+$\frac{5}{2}$×3+1,…,可得第n个五边形是:$\frac{3}{2}$×(n-1)2+$\frac{5}{2}$×(n-1)+1,据此求出第8个五边形是多少即可.
解答 解:∵第1个五边形是:1=$\frac{3}{2}$×02+$\frac{5}{2}$×0+1,
第2个五边形是:5=$\frac{3}{2}$×12+$\frac{5}{2}$×1+1,
第3个五边形是:12=$\frac{3}{2}$×22+$\frac{5}{2}$×2+1,
第4个五边形是:22=$\frac{3}{2}$×32+$\frac{5}{2}$×3+1,
…,
∴第n个五边形是:$\frac{3}{2}$×(n-1)2+$\frac{5}{2}$×(n-1)+1,
∴第8个五边形是:
$\frac{3}{2}$×(8-1)2+$\frac{5}{2}$×(8-1)+1
=$\frac{147}{2}$+$\frac{35}{2}$+1
=92
即第8个五边形是92.
点评 此题主要考查了图形的变化类问题,要熟练掌握,首先找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题,解答此题的关键是判断出:n个五边形是:$\frac{3}{2}$×(n-1)2+$\frac{5}{2}$×(n-1)+1.


科目:初中数学 来源: 题型:选择题
| A. | a-2=-a2 | B. | a+a2=a3 | C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | (a2)3=a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 居民(户) | 1 | 2 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 中位数是50 | B. | 众数是51 | C. | 方差是42 | D. | 极差是21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 直线条数 | 图形 | 最多交点个数 |
| 1 |  | 1 |
| 2 |  | 3=1+2 |
| 3 |  | 6=1+2+3 |
| 4 |  | 10=1+2+3+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
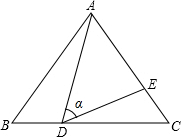 如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且$cosa=\frac{4}{5}$.下列结论:
如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且$cosa=\frac{4}{5}$.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com