分析 （1）根据待定系数法，可得函数解析式；根据自变量的值，可得相应的函数值，根据四边形对角线的关系，可得答案；
（2）根据对称性，可得AC的长，根据顶点式解析式，可得F2根据待定系数法，可得4a+c-1=c，根据四边形的面积公式，可得答案；
（3）分类讨论：B在A的右侧，B在A的左侧，AC=2$\sqrt{3}$，BD=2，可得答案．
解答 解：（1）由A、C点关于对称轴对称，得
对称轴x=1．
将C点坐标代入解析式，及对称轴公式，得
$\left\{\begin{array}{l}{-\frac{b}{2a}=1}\\{4a+2b=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$，
故答案为：1，-2；
当x=1时，y=x2，B（1，1）；
y=x2-2x=-1，D（1，-1），
四边形ABCD的对角线相等互相平分，且互相垂直，
四边形ABCD是正方形，
故选：D．
（2）∵B（2，c-1），
∴AC=2×2=4．
∵当x=0，y=c，
∴A（0，c）．
∵F1：y=ax2+c，B（2，c-1）．
∴设F2：y=a（x-2）2+c-1．
∵点A（0，c）在F2上，
∴4a+c-1=c，
∴$a=\frac{1}{4}$．
当x=2时，y=ax2+c=4a+c，B（2，4a+c）
∴BD=（4a+c）-（c-1）=2．
∴S四边形ABCD=$\frac{1}{2}$AC•BD=4．
（3）如图所示
，
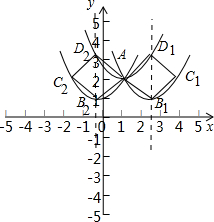y=$\frac{1}{3}{x^2}-\frac{2}{3}x+\frac{7}{3}$=$\frac{1}{3}$（x-1）2+2
设F2的解析式y=$\frac{1}{3}$（x-1-a）2+2+b，
B（1+a，2+b），C（3b+1+a，2），D（1+a，$\frac{1}{3}$a2+2）．
B点在A点的右侧时，$\frac{1}{2}$AC=1+a-1=$\sqrt{3}$，BD=$\frac{1}{3}$a2+2-2-b=2，
解得a=$\sqrt{3}$，b=-1，B1（1+$\sqrt{3}$，1），
B在点A的左侧时，$\frac{1}{2}$AC=1-（a+1）=$\sqrt{3}$，BD=$\frac{1}{3}$a2+2-2-b=2，
解得a=-$\sqrt{3}$，b=-1，B2（1-$\sqrt{3}$，1），
综上所述：B1（$1+\sqrt{3}$，1），B2（$1-\sqrt{3}$，1）．
点评 本题考察了二次函数综合题，利用待定系数法求函数解析式，又利用了正方形的判定；（2）利用待定系数法求出a，利用自变量与函数值的关系求出B点坐标，利用对角线互相垂直四边形的面积公式；（3）利用了图象的平移法，利用自变量与函数值的关系，确定C、D点坐标，又利用两点间的距离得出a、b的值，分类讨论是解题关键，以防遗漏．
科目：初中数学 来源： 题型：选择题
| x | -1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | -1 | -1 | 1 |
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
古希腊人用石子在沙滩上摆成各种形状来研究，如，一，五，十二，二十二…为五边形，则8个五边形是多少？