
【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是【 】
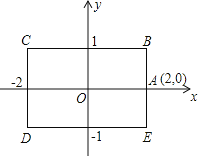
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
【答案】D。
【解析】利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每
一次相遇的地点,找出规律作答:
∵ 矩形的边长为4和2,物体乙是物体甲的速度的2倍,时间相同,
∴物体甲与物体乙的路程比为1:2。由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×![]() =4,物体乙行的路程为12×
=4,物体乙行的路程为12×![]() =8,在BC边相遇;
=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×![]() =8,物体乙行的路程为12×2×
=8,物体乙行的路程为12×2×![]() =16,在DE边相遇;
=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×![]() =12,物体乙行的路程为12×3×
=12,物体乙行的路程为12×3×![]() =24,在A点相遇;
=24,在A点相遇;
…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2012÷3=670…2,
故两个物体运动后的第2012次相遇地点的是:第二次相遇地点,即物体甲行的路程为12×2×![]() =8,物体乙行的路程为12×2×
=8,物体乙行的路程为12×2×![]() =16,在DE边相遇。
=16,在DE边相遇。
此时相遇点的坐标为:(-1,-1)。故选D。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AC和AB上的点,BD与CE相交于点O,给出下列四个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.

(1)上述四个条件中,由哪两个条件可以判定AB=AC?(用序号写出所有的情形)
(2)选择(1)小题中的一种情形,说明AB=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电专卖店销售每台进价分别200元、160元的A,B两种型号的电风扇,下表是近两周的销售情况
销售时段 | 销售数量 | 销售收入 | |
A 种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1550 元 |
第二周 | 4台 | 8台 | 2600 元 |
(进价、售价均保持不变,利销=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价;
(2)若专卖店准备用不多于3560元的金额再采购这两种型号的电风扇共20台,且采购A型电风扇的数量不少于8台.求专卖店有哪几种采购方案?
(3)在(2)的条件下.如果采购的电风扇都能销售完,请直接写出哪种采购方案专卖店所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①单项式-![]() 的系数为-
的系数为-![]() ,次数为2;②90°的角叫余角,180°的角叫补角③若AC=BC,则点C是线段AB的中点;④经过一点有且只有一条直线与这条直线平行,其中错误的说法有( )
,次数为2;②90°的角叫余角,180°的角叫补角③若AC=BC,则点C是线段AB的中点;④经过一点有且只有一条直线与这条直线平行,其中错误的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y= ![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,6),则△AOC的面积为 .
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,6),则△AOC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分类讨论是一种非常重要的数学方法,如果一道题提供的已知条件中包含几种情况,我们可以分情况讨论来求解.例如:若|x|=2,|y|=3求x+y的值.
情况①若x=2,y=3时,x+y=5
情况②若x=2,y=﹣3时,x+y=﹣1
情况③若x=﹣2,y=3时,x+y=1
情况④若x=﹣2,y=﹣3时,x+y=﹣5
所以,x+y的值为1,﹣1,5,﹣5.
几何的学习过程中也有类似的情况:
问题(1):已知点A,B,C在一条直线上,若AB=8,BC=3,则AC长为多少?
通过分析我们发现,满足题意的情况有两种
情况①当点C在点B的右侧时,如图1,此时,AC=
情况②当点C在点B的左侧时,如图2,此时,AC=
通过以上问题,我们发现,借助画图可以帮助我们更好的进行分类.
问题(2):如图3,数轴上点A和点B表示的数分别是﹣1和2,点C是数轴上一点,且BC=2AB,则点C表示的数是多少?
仿照问题1,画出图形,结合图形写出分类方法和结果.
问题(3):点O是直线AB上一点,以O为端点作射线OC、OD,使∠AOC=60°,OCOD,求∠BOD的度数.画出图形,直接写出结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分12分)
直线y=![]() x+6和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作长方形ABCD,AB:BC=3:4.
x+6和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作长方形ABCD,AB:BC=3:4.
(1)当点A与点F重合时(图1),求证:四边形ADBE是平行四边形,并求直线DE的表达式;
(2)当点A不与点F重合时(图2),四边形ADBE仍然是平行四边形?说明理由,此时你还能求出直线DE的表达式吗?若能,请你出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价1000元,领带每条定价200元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;②西装和领带都按定价的90%付款.现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)若该客户按方案①购买,需付款多少元;(用含x的代数式表示)若该客户按方案②购买,需付款多少元.(用含x的代数式表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30,你能给出一种更为省钱的购买方案吗?若有,请写出你的购买方案和总费用;若无,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com