Question

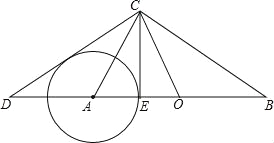
【题目】如图所示，在Rt△ABC与Rt△OCD中，∠ACB=∠DCO=90°，O为AB的中点．

（1）求证：∠B=∠ACD．

（2）已知点E在AB上，且BC2=ABBE．

（i）若tan∠ACD=，BC=10，求CE的长；

（ii）试判定CD与以A为圆心、AE为半径的⊙A的位置关系，并请说明理由．

Answer 1

【答案】(1)详见解析；（2）（i）CE=6；（ii）详见解析.

【解析】

试题分析：（1）因为∠ACB=∠DCO=90°，所以∠ACD=∠OCB，又因为点O是Rt△ACB中斜边AB的中点，所以OC=OB，所以∠OCB=∠B，利用等量代换可知∠ACD=∠B；（2）（i）因为BC2=ABBE，所以△ABC∽△CBE，所以∠ACB=∠CEB=90°，因为tan∠ACD=tan∠B，利用勾股定理即可求出CE的值；（ii）过点A作AF⊥CD于点F，易证∠DCA=∠ACE，即可得CA是∠DCE的平分线，所以AF=AE，所以直线CD与⊙A相切．

试题解析：（1）∵∠ACB=∠DCO=90°，

∴∠ACB﹣∠ACO=∠DCO﹣∠ACO，

即∠ACD=∠OCB，

又∵点O是AB的中点，

∴OC=OB，

∴∠OCB=∠B，

∴∠ACD=∠B，

（2）（i）∵BC2=ABBE，

∴，

∵∠B=∠B，

∴△ABC∽△CBE，

∴∠ACB=∠CEB=90°，

∵∠ACD=∠B，

∴tan∠ACD=tan∠B=，

设BE=4x，CE=3x，

由勾股定理可知：BE2+CE2=BC2，

∴（4x）2+（3x）2=100，

∴解得x=2，

∴CE=6；

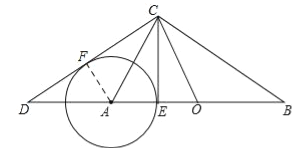
（ii）过点A作AF⊥CD于点F，

∵∠CEB=90°，

∴∠B+∠ECB=90°，

∵∠ACE+∠ECB=90°，

∴∠B=∠ACE，

∵∠ACD=∠B，

∴∠ACD=∠ACE，

∴CA平分∠DCE，

∵AF⊥CE，AE⊥CE，

∴AF=AE，

∴直线CD与⊙A相切．