
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在![]() 轴上.
轴上.

(1)求m的值及这个二次函数的解析式;
(2)若P(![]() ,0) 是
,0) 是![]() 轴上的一个动点,过P作
轴上的一个动点,过P作![]() 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<![]() < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
【答案】(1) ![]() ;
;![]() (2)①
(2)①![]() 有最大值
有最大值![]() ②存在.(2,0)(
②存在.(2,0)(![]() ,0)(
,0)(![]() ,0).
,0).
【解析】
(1)将A点坐标分别代入抛物线的直线,便可求出抛物线的解析式和m的值;
(2)过A作AH⊥PM于H,利用△MAB的面积=S梯形BOHA-S△BOM-S△AMH计算即可;
(3)①线段DE的长为h,根据P点坐标分别求出DE两点坐标,便可求出h与a之间的函数关系式,进而可求出线段DE的最大值;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,要使四边形NMED是平行四边形,必须DE=MN=2,由①知DE=|-a2+3a|,进而求出a的值,所以P的坐标可求出.
(1)设抛物线的解析式为y=a(x-1)2,
∵点A(3,4)在抛物线上,则4=a(3-1)2,
解得a=1,
∴抛物线的解析式为y=(x-1)2
∵点A(3,4)也在直线y=x+m,即4=3+m,
解得m=1;
(2)过A作AH⊥PM于H,
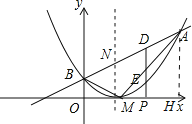
∵B(0,1),M(1,0),A(3,4),
∴OB=1,OH=3,AH=4,
∴△MAB的面积=S梯形BOHA-S△BOM-S△AMH=7.5-![]() ×1×1-
×1×1-![]() ×2×4=3;
×2×4=3;
(3)①已知P点坐标为P(a,0),则E点坐标为E(a,a2-2a+1),D点坐标为D(a,a+1),
h=DE=yD-yE=a+1-(a2-2a+1)=-a2+3a,
∴h与a之间的函数关系式为h=-a2+3a=-(a-![]() )2+
)2+![]() (0<a<3),
(0<a<3),
∴线段DE的最大值是![]() ;
;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,
理由是∵M(1,0),
∴把x=1代入y=x+1得:y=2,
即N(1,2),
∴MN=2,
要使四边形NMED是平行四边形,必须DE=MN=2,
由①知DE=|-a2+3a|,
∴2=|-a2+3a|,
解得:a1=2,a2=1,a3=![]() ,a4=
,a4=![]() ,
,
∴(2,0),(1,0)(因为和M重合,舍去)(![]() ,0),(
,0),(![]() ,0)
,0)
∴P的坐标是(2,0),(![]() ,0),(
,0),(![]() ,0).
,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.
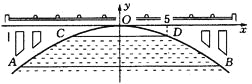
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,抛物线![]() (b为常数)的对称轴是直线x=1.
(b为常数)的对称轴是直线x=1.
(1)求该抛物线的表达式;
(2)点A(8,m)在该抛物线上,它关于该抛物线对称轴对称的点为A',求点A'的坐标;
(3)选取适当的数据填入下表,并在如图5所示的平面直角坐标系内描点,画出该抛物线.
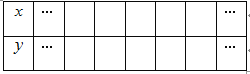

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
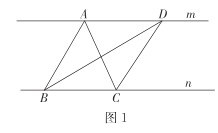
(1)如图1,![]() 的边BC在直线n上,过顶点A作直线m∥n,在直线m上任取一点D连接BD,CD,则
的边BC在直线n上,过顶点A作直线m∥n,在直线m上任取一点D连接BD,CD,则![]() 的面积_______
的面积_______![]() 的面积(填“等于”大于”或“小于”)
的面积(填“等于”大于”或“小于”)
问题探究
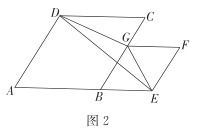
(2)如图2,在菱形ABCD和菱形BGFE中,![]() ,求
,求![]() 的面积.
的面积.
问题解决
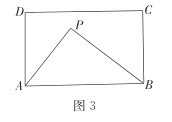
(3)如图3在矩形ABCD中,![]() ,在矩形ABCD内(可以在边上)存在点P,使得
,在矩形ABCD内(可以在边上)存在点P,使得![]() 的面积等于矩形ABCD的面积的
的面积等于矩形ABCD的面积的![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,A(1,7)、B(5,5)、C(7,5)、D(5,1).
(1)将线段AB绕点B逆时针旋转,得到对应线段BE.当BE与CD第一次平行时,画出点A运动的路径,并直接写出点A运动的路径长;
(2)线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,直接写出这个旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,以BC为弦的⊙O分别与AB,AC交于点D和E,点F是BC延长线上一点,CF=AE,连接EF.
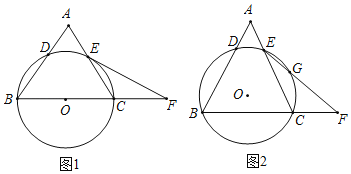
(1)如图1,BC为直径,求证:EF是⊙O的切线;
(2)如图2,EF与⊙O交于点G,⊙O的半径为1,BC的长为![]() π,求BF的长.
π,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知![]() ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如![]() 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.

请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”![]() ,必有实数根;
,必有实数根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6![]() ,求ABC 的面积.
,求ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A、B在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=
(k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=![]() ,则k的值_____.
,则k的值_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
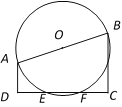
【题目】如图,梯形ABCD中,AD∥BC,∠ADC=90,AD= 2,BC= 4,![]() .以AB为直径作⊙O,交边DC于E、F两点.
.以AB为直径作⊙O,交边DC于E、F两点.
(1)求证:DE=CF.
(2)求直径AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com