
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–Έ ACDE «÷ΛΟςΙ¥Ι…Ε®άμ ±”ΟΒΫΒΡ“ΜΗωΆΦ–ΈΘ§a ΓΔb ΓΔc « RtABCΚΆ RtBED ΒΡ±Ώ≥ΛΘ§“―÷Σ![]() Θ§’β ±Έ“Ο«Α―ΙΊ”Ύ x ΒΡ–Έ»γ
Θ§’β ±Έ“Ο«Α―ΙΊ”Ύ x ΒΡ–Έ»γ![]() Εΰ¥ΈΖΫ≥Χ≥ΤΈΣΓΑΙ¥œΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±Θ°
Εΰ¥ΈΖΫ≥Χ≥ΤΈΣΓΑΙ¥œΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±Θ°

«κΫβΨωœ¬Ν–Έ ΧβΘΚ
(1)–¥≥ω“ΜΗωΓΑΙ¥œΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±ΘΜ
(2)«σ÷ΛΘΚΙΊ”Ύ x ΒΡΓΑΙ¥œΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±![]() Θ§±Ί”– Β ΐΗυΘΜ
Θ§±Ί”– Β ΐΗυΘΜ
(3)»τ x 1 «ΓΑΙ¥œΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ± ![]() ΒΡ“ΜΗωΗυΘ§«“ΥΡ±Ώ–Έ ACDE ΒΡ÷ή≥Λ «6
ΒΡ“ΜΗωΗυΘ§«“ΥΡ±Ώ–Έ ACDE ΒΡ÷ή≥Λ «6![]() Θ§«σABC ΒΡΟφΜΐΘ°
Θ§«σABC ΒΡΟφΜΐΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() (¥πΑΗ≤ΜΈ®“Μ)Θ®2Θ©ΦϊΫβΈωΘ®3Θ©1.
(¥πΑΗ≤ΜΈ®“Μ)Θ®2Θ©ΦϊΫβΈωΘ®3Θ©1.
ΓΨΫβΈωΓΩ
Θ®1Θ©÷±Ϋ”’““ΜΉιΙ¥Ι… ΐ¥ζ»κΖΫ≥ΧΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίΗυΒΡ≈–±π ΫΦ¥Ω…«σΫβΘΜ
Θ®3Θ©ΗυΨίΖΫ≥ΧΒΡΫβ¥ζ»κ«σ≥ωa,b,cΒΡΙΊœΒΘ§‘ΌΗυΨίΆξ»ΪΤΫΖΫΙΪ ΫΒΡ±δ–ΈΫχ––«σΫβ.
Θ®1Θ©Β±a=3,b=4,c=5 ±Θ§
Ι¥œΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©“άΧβ“βΒΟΓς=Θ®![]() Θ©2-4ab=2c2-4ab,
Θ©2-4ab=2c2-4ab,
ΓΏa2+b2=c2,Γύ2c2-4ab=2Θ®a2+b2Θ©-4ab=2Θ®a-bΘ©2Γί0Θ§
Φ¥ΓςΓί0Θ§Ι ΖΫ≥Χ±Ί”– Β ΐΗυΘΜ
Θ®3Θ©Α―x=-1¥ζ»κΒΟa+b=![]() c
c
ΓΏΥΡ±Ώ–Έ ACDE ΒΡ÷ή≥Λ «6![]() Θ§
Θ§
Φ¥2(a+b)+ ![]() c=6
c=6![]() Θ§Ι ΒΟΒΫc=2Θ§
Θ§Ι ΒΟΒΫc=2Θ§
Γύa2+b2=4Θ§a+b=2![]()
ΓΏ(a+b)2= a2+b2+2ab
Γύab=2,
Ι ABC ΒΡΟφΜΐΈΣ![]() ab=1.
ab=1.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–ΓΉσΆ§―ßœκάϊ”Ο”Α≥Λ≤βΝΩ―ß–ΘΤλΗΥΒΡΗΏΕ»Θ§»γΆΦΘ§Υΐ‘ΎΡ≥“Μ ±ΩΧΝΔ“Μ≥ΛΕ»ΈΣ1ΟΉΒΡ±ξΗΥΘ§≤βΒΟΤδ”Α≥ΛΈΣ![]() ΟΉΘ§Ά§ ±ΤλΗΥΆΕ”ΑΒΡ“Μ≤ΩΖ÷‘ΎΒΊ…œΘ§Νμ“Μ≤ΩΖ÷‘ΎΡ≥“ΜΫ®÷ΰΈοΒΡ«Ϋ…œΘ§≤βΒΟΤλΗΥ”κΫ®÷ΰΈοΒΡΨύάκΈΣ10ΟΉΘ§ΤλΗΥ‘Ύ«Ϋ…œΒΡ”ΑΗΏΈΣ2ΟΉΘ§«κΑο–ΓΉσΆ§―ßΥψ≥ω―ß–ΘΤλΗΥΒΡΗΏΕ»Θ°
ΟΉΘ§Ά§ ±ΤλΗΥΆΕ”ΑΒΡ“Μ≤ΩΖ÷‘ΎΒΊ…œΘ§Νμ“Μ≤ΩΖ÷‘ΎΡ≥“ΜΫ®÷ΰΈοΒΡ«Ϋ…œΘ§≤βΒΟΤλΗΥ”κΫ®÷ΰΈοΒΡΨύάκΈΣ10ΟΉΘ§ΤλΗΥ‘Ύ«Ϋ…œΒΡ”ΑΗΏΈΣ2ΟΉΘ§«κΑο–ΓΉσΆ§―ßΥψ≥ω―ß–ΘΤλΗΥΒΡΗΏΕ»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ Χβ«ιΨ≥ΘΚ»γΆΦ1Θ§ABΓΈCDΘ§ ![]() ,
,![]() Θ°«σ
Θ°«σ![]() Ε» ΐΘ°
Ε» ΐΘ°
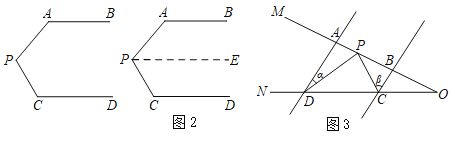
–ΓΟςΒΡΥΦ¬Ζ «ΘΚ»γΆΦ2Θ§ΙΐPΉςPEΓΈABΘ§Ά®ΙΐΤΫ––œΏ–‘÷ Θ§Ω…ΒΟ![]() _______Θ°
_______Θ°
Έ Χβ«®“ΤΘΚ»γΆΦ3Θ§ADΓΈBCΘ§ΒψP‘Ύ…δœΏOM…œ‘ΥΕ·Θ§ ![]() Θ§
Θ§ ![]() Θ°
Θ°
Θ®1Θ©Β±ΒψP‘ΎAΓΔBΝΫΒψ÷°Φδ‘ΥΕ· ±Θ§ ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷°Φδ”–ΚΈ ΐΝΩΙΊœΒΘΩ«κΥΒΟςάμ”….
÷°Φδ”–ΚΈ ΐΝΩΙΊœΒΘΩ«κΥΒΟςάμ”….
Θ®2Θ©»γΙϊΒψP‘ΎAΓΔBΝΫΒψΆβ≤ύ‘ΥΕ· ±Θ®ΒψP”κΒψAΓΔBΓΔO»ΐΒψ≤Μ÷ΊΚœΘ©Θ§«κΡψ÷±Ϋ”–¥≥ω![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
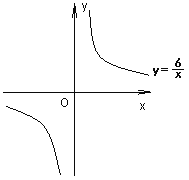
ΓΨΧβΡΩΓΩ»τΖ¥±»άΐΚ· ΐ![]() ”κ“Μ¥ΈΚ· ΐ
”κ“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœσΕΦΨ≠ΙΐΒψAΘ®
ΒΡΆΦœσΕΦΨ≠ΙΐΒψAΘ®![]() Θ§2Θ©
Θ§2Θ©
Θ®1Θ©«σΒψAΒΡΉχ±ξΘΜ
Θ®2Θ©«σ“Μ¥ΈΚ· ΐ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®3Θ©…ηOΈΣΉχ±ξ‘≠ΒψΘ§»τΝΫΗωΚ· ΐΆΦœώΒΡΝμ“ΜΗωΫΜΒψΈΣBΘ§«σΓςAOBΒΡΟφΜΐΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
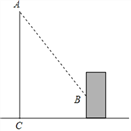
ΓΨΧβΡΩΓΩ“―÷Σ:ΒψA «ΥΪ«ζœΏ![]() ‘ΎΒΎ“Μœσœό…œΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”AO≤Δ―”≥ΛΫΜΝμ“ΜΖ÷÷ß”ΎΒψBΘ§“‘ABΈΣ“Μ±ΏΉςΒ»±Ώ»ΐΫ«–ΈABCΘ§ΒψC‘ΎΒΎΥΡœσœόΘ§ΥφΉ≈ΒψAΒΡ‘ΥΕ·Θ§ΒψCΒΡΈΜ÷Ο“≤≤ΜΕœΒΡ±δΜ·Θ§ΒΪ Φ÷’‘Ύ“ΜΚ· ΐΆΦœσ…œ‘ΥΕ·Θ§‘ρ’βΗωΚ· ΐΒΡΫβΈω Ϋ «( )
‘ΎΒΎ“Μœσœό…œΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”AO≤Δ―”≥ΛΫΜΝμ“ΜΖ÷÷ß”ΎΒψBΘ§“‘ABΈΣ“Μ±ΏΉςΒ»±Ώ»ΐΫ«–ΈABCΘ§ΒψC‘ΎΒΎΥΡœσœόΘ§ΥφΉ≈ΒψAΒΡ‘ΥΕ·Θ§ΒψCΒΡΈΜ÷Ο“≤≤ΜΕœΒΡ±δΜ·Θ§ΒΪ Φ÷’‘Ύ“ΜΚ· ΐΆΦœσ…œ‘ΥΕ·Θ§‘ρ’βΗωΚ· ΐΒΡΫβΈω Ϋ «( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2019≈°≈≈ άΫγ±≠”Ύ9‘¬14‘¬÷Ν29»’‘Ύ»’±ΨΨΌ––Θ§»ϋ÷ΤΈΣΒΞ―≠ΜΖ±»»ϋΘ®Φ¥ΟΩΝΫΗωΕ”÷°Φδ±»»ϋ“Μ≥ΓΘ©Θ§“ΜΙ≤±»»ϋ66≥ΓΘ§÷–Ιζ≈°≈≈“‘»Ϊ Λ≥…Φ®ΈάΟα άΫγ±≠ΙΎΨϋΘ§ΈΣΙζ«λ70÷ήΡξœΉ…œ¥σάώΘ§‘ρ÷–ΙζΕ”‘Ύ±ΨΫλ άΫγ±≠±»»ϋ÷–Ν§ ΛΘ® Θ©
A.10≥ΓB.11≥ΓC.12≥ΓD.13≥Γ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΤΥψ
Θ®1Θ©![]()
Θ®2Θ©Θ®+6Θ©-Θ®+12Θ©+Θ®+9Θ°6Θ©-Θ®+7Θ°6Θ©
Θ®3Θ©5ΓΝ![]() ®D
®D![]() ΓΝ
ΓΝ![]()
Θ®4Θ©Θ®![]() Θ©ΓΝ(Θ≠60 )
Θ©ΓΝ(Θ≠60 )
Θ®5Θ©Θ®2![]() )-(+10
)-(+10![]() )+(-8
)+(-8![]() )-(+3)
)-(+3)
Θ®6Θ©©¹14©¹Θ®1©¹0.5Θ©ΓΝ![]() ΓΝ[1©¹Θ®©¹2Θ©2]ΘΜ
ΓΝ[1©¹Θ®©¹2Θ©2]ΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐy=ax2+bx+c+2ΒΡΆΦœσ»γΆΦΥυ ΨΘ§ΕΞΒψΈΣΘ®©¹1Θ§0Θ©Θ§œ¬Ν–Ϋα¬έΘΚΔΌabcΘΦ0ΘΜΔΎb2©¹4ac=0ΘΜΔέaΘΨ2ΘΜΔή4a©¹2b+cΘΨ0Θ°Τδ÷–’ΐ»ΖΫα¬έΒΡΗω ΐ «Θ® Θ©
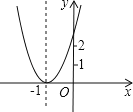
AΘ°1 BΘ°2 CΘ°3 DΘ°4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘”ΦΦΆ≈Ϋχ––‘”ΦΦ±μ―ίΘ§―ί‘±¥”θΈθΈΑε”“ΕΥA¥ΠΒ·ΧχΒΫ»ΥΧίΕΞΕΥ“ΈΉ”B¥ΠΘ§Τδ…μΧε(Ω¥≥…“ΜΒψ)ΒΡ¬ΖœΏ «≈ΉΈοœΏ![]() ΒΡ“Μ≤ΩΖ÷Θ§»γΆΦ
ΒΡ“Μ≤ΩΖ÷Θ§»γΆΦ
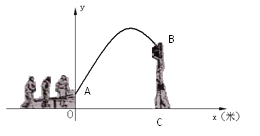
Θ®1Θ©«σ―ί‘±Β·ΧχάκΒΊΟφΒΡΉν¥σΗΏΕ»ΘΜ
Θ®2Θ©“―÷Σ»ΥΧίΗΏBCΘΫ3.4ΟΉΘ§‘Ύ“Μ¥Έ±μ―ί÷–Θ§»ΥΧίΒΫΤπΧχΒψAΒΡΥ°ΤΫΨύάκ «4ΟΉΘ§Έ ’β¥Έ±μ―ί «Ζώ≥…ΙΠΘΩ«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com