
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
运动项目 | 频数 |
羽毛球 | 30 |
篮球 | a |
乒乓球 | 36 |
排球 | b |
足球 | 12 |
请根据以上图表信息解答下列问题:
![]() 频数分布表中的
频数分布表中的![]() ______,
______,![]() ______;
______;
![]() 在扇形统计图中,“排球”所在的扇形的圆心角为______度;
在扇形统计图中,“排球”所在的扇形的圆心角为______度;
![]() 全校有多少名学生选择参加乒乓球运动?
全校有多少名学生选择参加乒乓球运动?

【答案】 24 18 54
(3)360人
【解析】分析:(1)根据选择乒乓球运动的人数是36人,对应的百分比是30%,即可求得总人数,然后利用百分比的定义求得a,用总人数减去其它组的人数求得b;
(2)利用360°乘以对应的百分比即可求得;
(3)求得全校总人数,然后利用总人数乘以对应的百分比求解.
详解:(1)抽取的人数是36÷30%=120(人),
则a=120×20%=24,
b=120-30-24-36-12=18.
故答案是:24,18;
(2)“排球”所在的扇形的圆心角为360°×18120=54°,
故答案是:54;
(3)全校总人数是120÷10%=1200(人),
则选择参加乒乓球运动的人数是1200×30%=360(人).


科目:初中数学 来源: 题型:
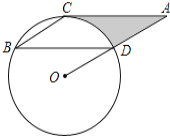
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=4![]() .
.
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
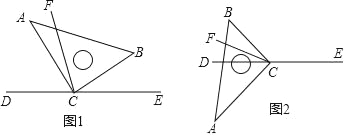
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓宽销售渠道,某水果商店计划将146个柚子和400个橙子装入大、小两种礼箱进行出售,其中每件小礼箱装2个柚子和4个橙子;每件大礼箱装3个柚子和9个橙子.要求每件礼箱都装满,柚子恰好全部装完,橙子有剩余,设小礼箱的数量为x件.
(1)大礼箱的数量为________件(用含x的代数式表示).
(2)若橙子剩余12个,则需要大、小两种礼箱共多少件?
(3)由于橙子有剩余,则小礼箱至少需要________件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
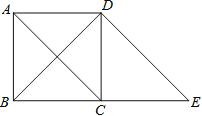
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
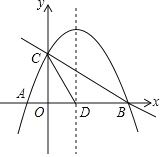
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 、B两点,与y轴交于点
、B两点,与y轴交于点![]() ,抛物线的对称轴交x轴于点D.
,抛物线的对称轴交x轴于点D.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的值;
的值;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
![]() 点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
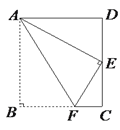
【题目】如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处, 折痕为AF,若CD=6,则AF等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是学习初中数学的- -个重要工具利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:数轴上点![]() 、点
、点![]() 表示的数为
表示的数为![]() ,则
,则![]() 两点之间的距离
两点之间的距离![]() ,若
,若![]() ,则可简化为;
,则可简化为;![]() 线段
线段![]() 的中点
的中点![]() 表示的数为
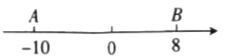
表示的数为![]() 如图,已知数轴上有
如图,已知数轴上有![]() 两点,分别表示的数为
两点,分别表示的数为![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴向右匀速运动,点
个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒
以每秒![]() 个单位长度向左匀速运动,设运动时间为
个单位长度向左匀速运动,设运动时间为![]() 秒
秒![]() .
.
(1)运动开始前,![]() 两点的距离为多少个单位长度;线段
两点的距离为多少个单位长度;线段![]() 的中点
的中点![]() 所表示的数为?
所表示的数为?
(2)点![]() 运动
运动![]() 秒后所在位置的点表示的数为 ;点
秒后所在位置的点表示的数为 ;点 ![]() 运动
运动![]() 秒后所在位置的点表示的数为 . (用含
秒后所在位置的点表示的数为 . (用含![]() 的式子表示
的式子表示
(3)它们按上述方式运动,![]() 两点经过多少秒会相距
两点经过多少秒会相距![]() 个单位长度?
个单位长度?
(4)若![]() 按上述方式运动,
按上述方式运动, ![]() 两点经过多少秒,线段
两点经过多少秒,线段![]() 的中点
的中点![]() 与原点重合?
与原点重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
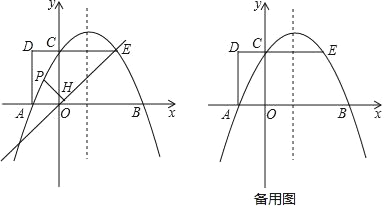
【题目】如图1,抛物线y=ax2+bx+2 与x轴交于A,B两点,与y轴交于点C,AB=4.矩形OADC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的表达式;
(2)点P是直线EO 上方抛物线上的一个动点,作PH⊥EO,垂足为H,求PH的最大值;
(3)点M在抛物线上,点N在抛物线的对称轴上,若四边形ACMN是平行四边形,求点M、N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com