
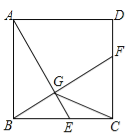
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为![]() .其中正确的说法是 .(把你认为正确的说法的序号都填上)
.其中正确的说法是 .(把你认为正确的说法的序号都填上)
【答案】②④.
【解析】
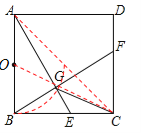
试题分析:∵在正方形ABCD中,AE、BD垂直平分,∴当E移动到与C重合时,AG=GE,故①错误;
∵BF⊥AE,∴∠AEB+∠CBF=90°,∵∠AEB+∠BAE=90°,∴∠BAE=∠CBF,在△ABE和△BCF中,∵∠BAE=∠CBF,∠ABE=∠BCF=90°,AB=BC,∴△ABE≌△BCF(AAS),∴故②正确;
根据题意,G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,∴圆弧BD的长=![]() =
=![]() ,故③错误;
,故③错误;
由于OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,OC=![]() =
=![]() =
=![]() ,CG的最小值为OC﹣OG=
,CG的最小值为OC﹣OG=![]() ,故④正确;
,故④正确;
综上所述,正确的结论有②④.故答案为:②④.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(﹣3,0),点C(0,4),作CD∥x轴交抛物线于点D,作DE⊥x轴,垂足为E,动点M从点E出发在线段EA上以每秒2个单位长度的速度向点A运动,同时动点N从点A出发在线段AC上以每秒1个单位长度的速度向点C运动,当一个点到达终点时,另一个点也随之停止运动,设运动时间为t秒.
经过点A(﹣3,0),点C(0,4),作CD∥x轴交抛物线于点D,作DE⊥x轴,垂足为E,动点M从点E出发在线段EA上以每秒2个单位长度的速度向点A运动,同时动点N从点A出发在线段AC上以每秒1个单位长度的速度向点C运动,当一个点到达终点时,另一个点也随之停止运动,设运动时间为t秒.
(1)求抛物线的解析式;
(2)设△DMN的面积为S,求S与t的函数关系式;
(3)①当MN∥DE时,直接写出t的值;
②在点M和点N运动过程中,是否存在某一时刻,使MN⊥AD?若存在,直接写出此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在正方形网格中,每个小方格都是边长为1的正方形,A和B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形的面积为1个平方单位,则C点的个数为( ). 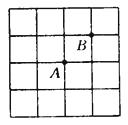
A.3个
B.4个
C.5个
D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列描述一次函数y=-2x+5图象性质错误的是( )
(A)y随x的增大而减小
(B)直线经过第一、二、四象限
(C)直线从左到右是下降的
(D)直线与x轴交点坐标是(0,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( ) 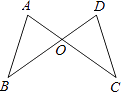
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠AOB=∠DOC
查看答案和解析>>
科目:初中数学 来源: 题型:
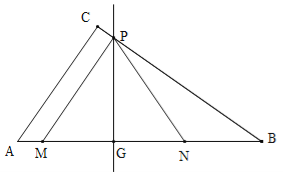
【题目】如图,在Rt△ABC中,∠ACB=900,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.
(1)当t= 秒时,动点M、N相遇;
(2)设△PMN的面积为S,求S与t之间的函数关系式;
(3)取线段PM的中点K,连接KA、KC,在整个运动过程中,△KAC的面积是否变化?若变化,直接写出它的最大值和最小值;若不变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com