
【题目】如图,抛物线![]() 经过点A(﹣3,0),点C(0,4),作CD∥x轴交抛物线于点D,作DE⊥x轴,垂足为E,动点M从点E出发在线段EA上以每秒2个单位长度的速度向点A运动,同时动点N从点A出发在线段AC上以每秒1个单位长度的速度向点C运动,当一个点到达终点时,另一个点也随之停止运动,设运动时间为t秒.
经过点A(﹣3,0),点C(0,4),作CD∥x轴交抛物线于点D,作DE⊥x轴,垂足为E,动点M从点E出发在线段EA上以每秒2个单位长度的速度向点A运动,同时动点N从点A出发在线段AC上以每秒1个单位长度的速度向点C运动,当一个点到达终点时,另一个点也随之停止运动,设运动时间为t秒.
(1)求抛物线的解析式;
(2)设△DMN的面积为S,求S与t的函数关系式;
(3)①当MN∥DE时,直接写出t的值;
②在点M和点N运动过程中,是否存在某一时刻,使MN⊥AD?若存在,直接写出此时t的值;若不存在,请说明理由.

【答案】(1)![]() ;(2)S=
;(2)S=![]() (0<t≤3);(3)①t=
(0<t≤3);(3)①t=![]() ;②t=
;②t=![]() .
.
【解析】(1)∵抛物线![]() 经过点A(﹣3,0),点C(0,4),∴
经过点A(﹣3,0),点C(0,4),∴ ,解得:
,解得:![]() ,即抛物线的解析式为:
,即抛物线的解析式为:![]() ;
;
(2)作NH⊥AM于点H,如由图1所示,∵![]() =
=![]() ,∴对称轴x=
,∴对称轴x=![]() ,∵点A(﹣3,0),点C(0,4),CD∥x轴交抛物线于点D,DE⊥x轴,垂足为E,∴点D(3,4),点E(3,0),OA=3,OC=4,∴AC=5,AE=6,CD=3,∵NH⊥AM,AN=tME=2t,∴△ANH∽△ACO,AM=6﹣2t,∴
,∵点A(﹣3,0),点C(0,4),CD∥x轴交抛物线于点D,DE⊥x轴,垂足为E,∴点D(3,4),点E(3,0),OA=3,OC=4,∴AC=5,AE=6,CD=3,∵NH⊥AM,AN=tME=2t,∴△ANH∽△ACO,AM=6﹣2t,∴![]() ,即
,即![]() ,得NH=0.8t,∴S=S梯形AECD﹣S△AMN﹣S△DME﹣S△CDN
,得NH=0.8t,∴S=S梯形AECD﹣S△AMN﹣S△DME﹣S△CDN
=![]() (3+6)×4-
(3+6)×4-![]() ×(6-2t)×0.8t-
×(6-2t)×0.8t-![]() ×2t×4-
×2t×4-![]() ×3×(4-0.8t)
×3×(4-0.8t)
=![]() ,即S与t的函数关系式是S=
,即S与t的函数关系式是S=![]() (0<t≤3);
(0<t≤3);
(3)①当MN∥DE时,t的值是![]() ,理由:如右图2所示
,理由:如右图2所示
∵MN∥DE,AE=6,AC=5,AO=3,∴AM=6﹣2t,AN=t,△AMN∽△AOC,∴![]() ,即
,即![]() ,解得,t=
,解得,t=![]() ;
;
②存在某一时刻,使MN⊥AD,此时t的值是![]() ,理由:如右图3所示,设过点A(﹣3,0),C(0,4)的直线的解析式为y=kx+b,则:
,理由:如右图3所示,设过点A(﹣3,0),C(0,4)的直线的解析式为y=kx+b,则:![]() ,得:
,得:![]() ,即直线AC的解析式为
,即直线AC的解析式为![]() ,∵NH=0.8t,∴点N的纵坐标为0.8t,将y=0.8t代入
,∵NH=0.8t,∴点N的纵坐标为0.8t,将y=0.8t代入![]() ,得x=0.6t﹣3,∴点N(0.6t﹣3,0.8t)
,得x=0.6t﹣3,∴点N(0.6t﹣3,0.8t)
∵点E(3,0),ME=2t,∴点M(3﹣2t,0),∵点A(﹣3,0),点D(3,4),点M(3﹣2t,0),点N(0.6t﹣3,0.8t),AD⊥MN,∴![]() ,解得:t=
,解得:t=![]() .
.



科目:初中数学 来源: 题型:
【题目】王老师对甲、乙两人五次数学成绩进行统计,两人平均成绩均为90分,方差S甲2=12,S乙2=51,则下列说法正确的是( )
A. 甲、乙两位同学的成绩一样稳定
B. 乙同学的成绩更稳定
C. 甲同学的成绩更稳定
D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
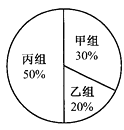
【题目】某年级组织学生参加夏令营,分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况.请你根据图中的信息回答下列问题:
报名人数分布直方图 报名人数扇形统计图
(1)求该年级报名参加本次活动的总人数;
(2)求该年级报名参加乙组的人数,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,那么,应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
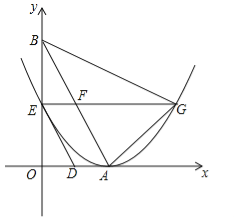
【题目】如图,直线![]() 与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和
与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和![]() 个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
(1)求点A,点B的坐标;
(2)用含t的代数式分别表示EF和AF的长;
(3)当四边形ADEF为菱形时,试判断△AFG与△AGB是否相似,并说明理由.
(4)是否存在t的值,使△AGF为直角三角形?若存在,求出这时抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果气温上升3度记作+3度,下降5度记作-5度,那么下列(1)+5度;(2)-6度; 各量分别表示什么?( )
A.上升5度;下降6度
B.上升6度;下降6度
C.上升5度;上升6度
D.下降5度;下降6度
查看答案和解析>>
科目:初中数学 来源: 题型:
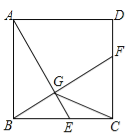
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为![]() .其中正确的说法是 .(把你认为正确的说法的序号都填上)
.其中正确的说法是 .(把你认为正确的说法的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com