
【题目】小芳同学有两根长度为4cm、10cm的木棒,她想钉一个三角形相框,桌上有五根木棒供她选择(如图所示),从中任选一根,能钉成三角形相框的概率是 . 
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进商品后,都加价40%作为销售价,元旦期间搞优惠促销,决定由顾客抽奖确定折扣,某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元,商场共盈利49元,甲、乙两种商品的进价分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,弦AB、CD相交于点E,连接AC、BC,AC=BC,AB=CD. 
(1)如图1,求证:BE平分∠CBD;
(2)如图2,F为BC上一点,连接AF交CD于点G,当∠FAB= ![]() ∠ACB时,求证:AC=BD+2CF;
∠ACB时,求证:AC=BD+2CF;
(3)如图3,在(2)的条件下,若S△ACF=S△CBD , ⊙O的半径为3 ![]() ,求线段GD的长.
,求线段GD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( ) 
A.abc<0
B.2a+b<0
C.a﹣b+c<0
D.4ac﹣b2<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2 ![]() ,反比例函数y=
,反比例函数y= ![]() (x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为 .
(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是反比例函数y= ![]() (k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
(k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= ![]() .
.
(1)k的值是;
(2)若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C. 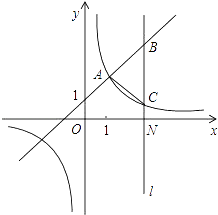
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com