若半径为5和4的两圆相交于A、B,且AB=6,则它们的圆心距d等于________.
4+

或4-

分析:有两种情况:两圆相外交,连接O
1O
2交AB与C点,连接O
1A、O
2A,再分别求出O
2C、O
1C的值,即可求得圆心距d;
两圆相内交时,连接O
1O
2并延长交AB与C点,连接O
1A、O
2A,再求出O
2C、O
1C的值,即可求得圆心距d.
解答:两圆相交有两种情况:
两圆相外交,连接O
1O
2交AB与C点,连接O
1A、O
2A,如下图所示,
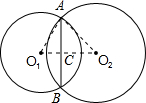
由题意知,AB=6,O
1A=4,O
2B=5;
∵AB为两圆交点,
∴O
1O
2垂直平分AB,
∴AC=3;
在Rt△O
1AC和Rt△O
2AC中,由勾股定理可得,
O
2C=4,O
1C=

,
所以,圆心距d=O
2C+O
1C=4+

;
两圆相内交时,连接O
1O
2并延长交AB与C点,连接O
1A、O
2A,如下图所示,

由题意可知,AB=6,O
1A=4,O
2A=5;
∵AB为两圆交点,
∴O
2C垂直平分AB,
∴AC=3;
在Rt△O
1AC和Rt△O
2AC中,由勾股定理可得,
O
2C=4,O
1C=

,
所以,圆心距d=O
2C-O
1C=4-

;
综上所述,圆心距d为4+

或4-

.
故此题应该填4+

或4-

.
点评:本题考查了相交两圆的性质.

 或4-
或4-
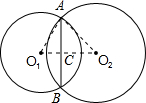
 ,
, ;
;
 ,
, ;
; 或4-
或4- .
. 或4-
或4- .
.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案