
【题目】已知反比例函数y=![]() (m为常数)的图像在第一、三象限.
(m为常数)的图像在第一、三象限.
(1)求m的取值范围.
(2)如图,若该反比例函数的图像经过ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0).
①求出该反比例函数的表达式;
②设P是该反比例函数图像上的一点,若OD=OP,则点P的坐标为________________;若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P有________个.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数 y=![]() 的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
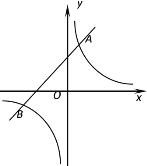
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;
(3)连接AO、BO,求△ABO的面积;
(4)在y轴上存在点P,使△AOP为等腰三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校有一块长方形空地,它的长和宽的比是3:1,面积为363![]() .
.
(1)求该长方形的长和宽;
(2)如图所示,工人师傅要在这块空地上设计一个圆形区域和四个扇形区域进行绿化,其中四个扇形区域的半径与中间圆形区域半径相同,若绿化区域的总面积为![]() ,请你帮助工人师傅计算一下中间圆形区域的直径.
,请你帮助工人师傅计算一下中间圆形区域的直径.
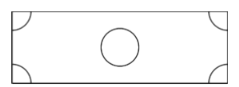
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数![]() 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某种产品展开图,高为3cm.
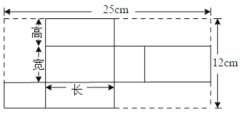
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
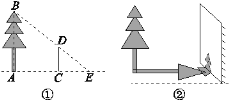
【题目】为了测量图①②中的树高,在同一时刻某人进行了如下操作:
图①:测得竹竿CD的长为0.8米,其影长CE为1米,树影AE长为2.4米.
图②:测得落在地面上的树的影长为2.8米,落在墙上的树影高1.2米.
请问图①和图②中的树高各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
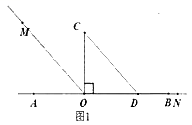
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
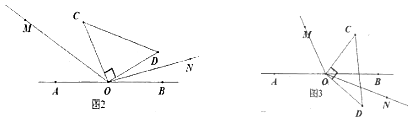
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区的6名志愿者,在“十一”假期组织区内的未成年学生到公园秋游,公园的门票为每人40元,现有两种优惠方案,甲方案:志愿者免费,未成年学生按8折收费;乙方案:志愿者和未成年学生都按7折收费,若有![]() 名未成年学生.
名未成年学生.
(1)当![]() 时,甲方案需 元;乙方案需 元;
时,甲方案需 元;乙方案需 元;
(2)用含![]() 的式子表示两种方案各需多少元?
的式子表示两种方案各需多少元?
(3)当![]() 为何值时,甲、乙两种方案是一样的.
为何值时,甲、乙两种方案是一样的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com