
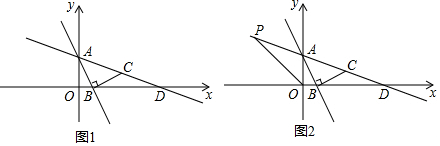
���� ��1�����ô���ϵ�������ɽ�����⣮
��2������C��CM��x����M���ɡ�AOB�ա�BMC���Ƴ���C������Ϊ��3��1���������ô���ϵ�������ɽ�����⣮
��3��A����P��ֱ��AC�ϣ��ҵ�P��������Ϊ3����y=3����y=-$\frac{1}{3}$x+2����x=-3������P��PN��y���ڵ�N���Ƴ�PN=3������S��OAP=$\frac{1}{2}$•OA•PN���㼴�ɣ�
B����P��ֱ��AC�ϣ���P��x��-$\frac{1}{3}$x+2������Ϊ��P�ڵڶ����ޣ���x�ᣬy�������ȣ���-x=-$\frac{1}{3}$x+2���Ƴ�PN=3������S��OAP=$\frac{1}{2}$•OA•NP���ɽ�����⣮
��4��A����ͼ3�У��Ե�B��D��QΪ��������������BCDȫ��ʱ����Q������������ͼ��ʾ��
B����ͼ4�У��Ե�B��D��QΪ��������������BCDȫ��ʱ����Q������������ͼ��ʾ��
��� �⣺��1����x=0����y=-2x+2�У���y=2��
���A��������0��2����
��y=0����y=-2x+2����-2x+2=0�����x=1��
���B��������1��0����
��2����ͼ1�У�����C��CM��x����M��
���AOB=��BMC=90�㣬
��AB��BC��
���ABC=90�㣬
���ABO+��CBM=90�㣬
�ߡ�ABO+��OAB=90�㣬
���OAB=��CBM��
�ڡ�AOB�͡�BMC�У�
$\left\{\begin{array}{l}{��OAB=��CBM}\\{��AOB=��CMB}\\{AB=BC}\end{array}\right.$��
���AOB�ա�BMC��
��BM=OA=2��CM=OB=1��
��OM=3��
���C��������3��1����
��ֱ��AC�Ľ���ʽΪy=kx+b����$\left\{\begin{array}{l}{b=2}\\{3k+b=1}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=2}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=-$\frac{1}{3}$x+2��
��3����ͼ2�У�
A���ߵ�P��ֱ��AC�ϣ��ҵ�P��������Ϊ3��
���y=3����y=-$\frac{1}{3}$x+2����x=-3��
����P��PN��y���ڵ�N��
��PN=3��
��S��OAP=$\frac{1}{2}$•OA•PN=$\frac{1}{2}$��2��3=3��
B���ߵ�P��ֱ��AC�ϣ�
��P��x��-$\frac{1}{3}$x+2����
�ߵ�P�ڵڶ����ޣ���x�ᣬy�������ȣ�
��-x=-$\frac{1}{3}$x+2��
��x=-3��
����P��PN��y���ڵ�N��
��PN=3��
��S��OAP=$\frac{1}{2}$•OA•NP=$\frac{1}{2}$��2��3=3��
��4��A����ͼ3�У��Ե�B��D��QΪ��������������BCDȫ��ʱ����Q������������ͼ��ʾ��
Q1��3��-1����Q2��4��-1����Q3��4��1����
B����ͼ4�У��Ե�B��D��QΪ��������������BCDȫ��ʱ����Q������������ͼ��ʾ��
Q1��8��1����Q2��2��3����Q3��7��-2����
����ʾ��C��CM��BD��M����Q2N��CM��N����֪��BCM�ա�CQ2N���ɴ˼������Q2���꣩
���� ���⿼��һ�κ����ۺ��⡢����ϵ�����������ε������ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����Ӹ����ߣ�����ȫ�������ν�����⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -6 | B�� | -8 | C�� | -12 | D�� | -18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | $\frac{2}{5}$ | D�� | $\frac{5}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ӯ���� | B�� | ӯ��10Ԫ | C�� | ����10Ԫ | D�� | ӯ��50Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 29��28 | B�� | 30��29 | C�� | 28��27 | D�� | 29��29 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com