
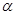 (
(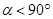 ),在旋转过程中:
),在旋转过程中: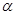 的度数为多少时,四边形APDQ是正方形?说明理由.
的度数为多少时,四边形APDQ是正方形?说明理由.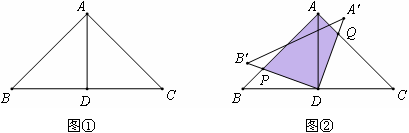
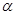 =45o
=45o S△AB C结合三角形的面积公式进行解答即可;
S△AB C结合三角形的面积公式进行解答即可;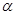 (
(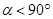 )怎样旋转,始终是△BPD≌△AQD,即四边形APDQ的面积等于S△ABD;
)怎样旋转,始终是△BPD≌△AQD,即四边形APDQ的面积等于S△ABD; S△ABC=
S△ABC= 
 =4
=4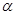 =45o时,四边形APDQ是正方形.
=45o时,四边形APDQ是正方形.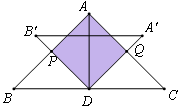
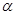 =45o时,DP⊥AB,即∠APD=90o
=45o时,DP⊥AB,即∠APD=90o

科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
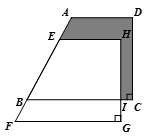
| A.绕点O旋转180° |
| B.先向上平移3格,再向右平移4格 |
| C.先以直线MN为对称轴作轴对称,再向上平移4格 |
| D.先向右平移4格,再以直线EF为对称轴作轴对称 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
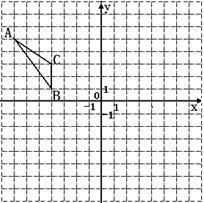
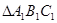 ,再将
,再将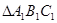 绕点
绕点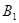 顺时针旋转90°得到
顺时针旋转90°得到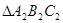 。
。
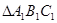 和
和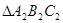 ;
;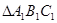 旋转时绕过的面积。
旋转时绕过的面积。查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
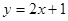 的图象与x轴交点的坐标为(
的图象与x轴交点的坐标为(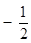 ,0),所以该函数的零点是
,0),所以该函数的零点是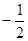 .
.
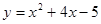 的零点是 ;
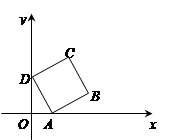
的零点是 ;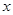 轴正方向滚动,即先以顶点A 为中心顺时针旋转,当顶点B落在
轴正方向滚动,即先以顶点A 为中心顺时针旋转,当顶点B落在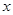 轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与
轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与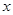 轴所围区域的面积为 .
轴所围区域的面积为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
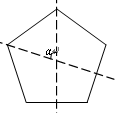
| A.75° | B.72° | C.70° | D.60° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 )时,设一直角边与x轴交于点E,另一直角边与y轴交于点F,在三角板绕点P旋转的过程中,使得△POE能否成为等腰三角形.请写出所有满足条件的点F的坐标 。
)时,设一直角边与x轴交于点E,另一直角边与y轴交于点F,在三角板绕点P旋转的过程中,使得△POE能否成为等腰三角形.请写出所有满足条件的点F的坐标 。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 经过怎样的平移得到
经过怎样的平移得到 ( )
( )
A.把 向左平移4个单位,再向下平移2个单位 向左平移4个单位,再向下平移2个单位 |
B.把 向右平移4个单位,再向下平移2个单位 向右平移4个单位,再向下平移2个单位 |
C.把 向右平移4个单位,再向上平移2个单位 向右平移4个单位,再向上平移2个单位 |
D.把 向左平移4个单位,再向上平移2个单位 向左平移4个单位,再向上平移2个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com