
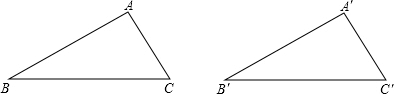
分析 延长BA、B′A′,使AD=AC,A′D′=A′C′,连接CD、C′D′,则∠D=∠ACD,∠D′=∠A′C′D′,证出BD=B′D′,由SAS证明△BCD≌△B′C′D′,得出对应角相等∠D=∠D′,∠BCD=∠B′C′D′,得出∠ACB=∠A′C′B′,再由ASA证明△ABC≌△A′B′C′即可.
解答 证明:延长BA、B′A′,使AD=AC,A′D′=A′C′,连接CD、C′D′,如图所示: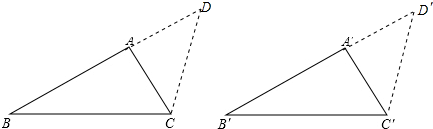 则∠D=∠ACD,∠D′=∠A′C′D′,∵AB+AC=A′B′+A′C′,
则∠D=∠ACD,∠D′=∠A′C′D′,∵AB+AC=A′B′+A′C′,
∴BD=B′D′,
在△BCD和△B′C′D′中,
$\left\{\begin{array}{l}{BD=B′D′}&{\;}\\{∠B=∠B′}&{\;}\\{BC=B′C′}&{\;}\end{array}\right.$,
∴△BCD≌△B′C′D′(SAS),
∴∠D=∠D′,∠BCD=∠B′C′D′,
∴∠ACB=∠A′C′B′,
在△ABC和△A′B′C′中,
$\left\{\begin{array}{l}{∠B=∠B′}&{\;}\\{BC=B′C′}&{\;}\\{∠ACB=∠A′C′B′}&{\;}\end{array}\right.$,
∴△ABC≌△A′B′C′(ASA).
点评 本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法,通过作辅助线证明三角形全等是解决问题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
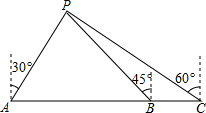 天宜号船向正东方航行(如图),船在A处时测得灯塔在P北偏东30°方向,前进到B处时测得灯塔P恰好在西北方向,又航行半小时到达C处,此时测得灯塔P在北偏西60°方向,若船速为每小时20海里,求A、C两点间的距离.
天宜号船向正东方航行(如图),船在A处时测得灯塔在P北偏东30°方向,前进到B处时测得灯塔P恰好在西北方向,又航行半小时到达C处,此时测得灯塔P在北偏西60°方向,若船速为每小时20海里,求A、C两点间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
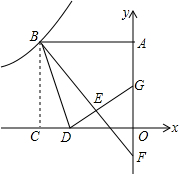 如图,正方形OABC的顶点A在y轴的正半轴上,顶点C在x轴的负半轴上,反比例函数y=-$\frac{9}{x}$在第二象限的图象经过点B,点D坐标为(-2,0),将正方形沿BD翻折,使点C落在E处,分别延长BE、DE角y轴于点F和G,则线段FG的长度是$\frac{5}{2}$.
如图,正方形OABC的顶点A在y轴的正半轴上,顶点C在x轴的负半轴上,反比例函数y=-$\frac{9}{x}$在第二象限的图象经过点B,点D坐标为(-2,0),将正方形沿BD翻折,使点C落在E处,分别延长BE、DE角y轴于点F和G,则线段FG的长度是$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是CD的中点,F在AB上,且∠1=∠2,AE、DF交于P,BE、CF交于Q,求证:四边形EPFQ是平行四边形.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是CD的中点,F在AB上,且∠1=∠2,AE、DF交于P,BE、CF交于Q,求证:四边形EPFQ是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com