
����Ŀ���͵�춯������һ�ֽ��͡��������¼���������������ʻ�����в���ԭ�����˷ѵ��������մ��������õ������У������ڵ�����ʻʱ��ʹ�����ش����綯��������������Լȼ�ͣ�ijƷ���͵�춯��������ͨ��������سɱ����ݹ������£�
�͵�춯���� | ��ͨ���� | |
����۸� | 17.48 | 15.98 |
ÿ�ٹ���ȼ�ͳɱ���Ԫ�� | 31 | 46 |
ij�˼ƻ�����һ������Ʒ�Ƶ���������������δ��10����ó��ɱ�����ֻ���dz��ۺ�ȼ�ͳɱ�������£�����ѡ���͵�춯�����ijɱ�������ѡ����ͨ�����ijɱ��������ڹ���ʱ��Ԥ��ƽ��ÿ����ʻ�Ĺ���������Ϊ��������
A. 5000 B. 10000 C. 15000 D. 20000

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾����A��B���ֻ�������������ij�ֻ����������ֻ����˳�����������������5Сʱ��A�ֻ�������ij��0ʱ��ʼ����������1Сʱ��B�ֻ�����Ҳ��ʼ��������ͼ���߶�OG��ʾA�ֻ����˵İ�����yA(ǧ��)��ʱ��x(ʱ)�ĺ���ͼ��������ͼ���ṩ����Ϣ���������������

(1)��yB����x�ĺ�������ʽ��
(2)���A��B���ֻ�������������5Сʱ����ôB�ֻ����˱�A�ֻ����˶�����˶���ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ����1��3��������4��1������2��1�����Ƚ���ABC��һȷ������ƽ�Ƶõ���A1B1C1 �� ��B�Ķ�Ӧ��B1�������ǣ�1��2�����ٽ���A1B1C1��ԭ��O˳ʱ����ת90��õ���A2B2C2 �� ��A1�Ķ�Ӧ��Ϊ��A2 �� 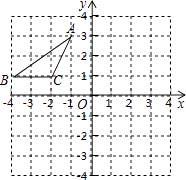
��1��������A1B1C1��
��2��������A2B2C2��
��3������������α任�����У���A������A1����A2��·���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���㣨2����4���ڷ���������y= ![]() ��ͼ���ϣ������и����ڴ˺���ͼ���ϵ��ǣ�������
��ͼ���ϣ������и����ڴ˺���ͼ���ϵ��ǣ�������
A.��2��4��
B.����1����8��
C.����2����4��
D.��4����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
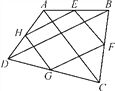
����Ŀ����ͼ��ʾ��E��F��G��H�ֱ����ı���ABCD�ı�AB��BC��CD��AD���е���
(1)���ı���ABCD�Ǿ���ʱ���ı���EFGH��_________����˵�����ɣ�
(2)���ı���ABCD����ʲô����ʱ���ı���EFGHΪ�����Σ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������м���ԭ��360ǧ�ˣ�����ԭ��290ǧ�ˣ��ƻ�����������ԭ������A��B���ֲ�Ʒ��50��.��֪����һ��A�ֲ�Ʒ���ü���ԭ��9ǧ�ˡ�����ԭ��3ǧ�ˣ��ɻ�����700Ԫ������һ��B�ֲ�Ʒ���ü���ԭ��4ǧ�ˡ�����ԭ��10ǧ�ˣ��ɻ�����1200Ԫ��������A�ֲ�Ʒ����������Ϊx�� A��B���ֲ�Ʒ����������Ϊy (Ԫ)
��1����д��y��x֮��ĺ�����ϵʽ��
��2������Ա���x��ȡֵ��Χ��
��3�����ú���������˵���������������������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������߾���A����1��0����B��5��0����C��0��- ![]() �����㣮
�����㣮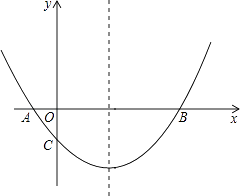
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ�������һ��P��ʹPA+PC��ֵ��С�����P�����ꣻ
��3����MΪx����һ���㣬�����������Ƿ����һ��N��ʹ��A��C��M��N�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ����N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ������4Ԫ/ǧ�˵ļ۸�һ��ˮ������������״�����ã��õ����ٴι���ͬһ��ˮ�����ڶ��ν����۸�ȵ�һ��ÿǧ�˱�����0.5Ԫ������ˮ������ǡ���ǵ�һ�ι���ˮ��������2����������ˮ�������ι���ˮ������ȥ��2200Ԫ.
(1)��ˮ�������ηֱ����˶���Ԫ��ˮ��?
(2)�������У��������ν����ļ۸�ͬ����ˮ����������ͬ�ļ۸��۳�������һ�ι�����ˮ����3%����ģ��ڶ��ι�����ˮ����5%����ģ���ˮ����ϣ��������Щˮ������������1244Ԫ�����ˮ��ÿǧ���ۼ�����Ϊ����Ԫ?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com