
【题目】(10分)在△ABC中,BE、CF分别是AC、AB两条边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。求证:AG=AD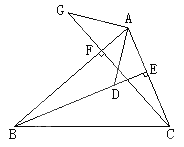
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°,若抛物线 y=x+k与扇形OAB的边界总有两个公共点,则实数取值范围是

A. -4<k<![]() B. -2<k<
B. -2<k<![]()
C. -4<k<![]() D. --2<k<
D. --2<k<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C= ![]() ,其中正确的有( )
,其中正确的有( ) 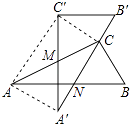
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
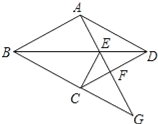
【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.
(1)求证:∠DAE=∠DCE;
(2)当CE=2EF时,EG与EF的等量关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com