
【题目】如图,![]() 中,
中,![]() 和
和![]() 分别平分
分别平分![]() 和
和![]() 的外角
的外角![]() ,一动点
,一动点![]() 在
在![]() 上运动,过点
上运动,过点![]() 作
作![]() 的平行线与
的平行线与![]() 和
和![]() 的角平分线分别交于点
的角平分线分别交于点![]() 和点
和点![]() .
.

![]() 求证:当点
求证:当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 为矩形,说明理由;
为矩形,说明理由;
![]() 在第
在第![]() 题的基础上,当
题的基础上,当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 为正方形,说明理由.
为正方形,说明理由.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
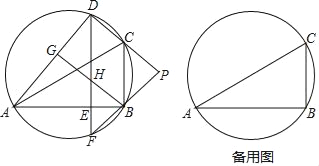
【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE、CE分别是∠ABC和∠ACB的平分线,过点E作DF∥BC交AB于D,交AC于F,若AB =5,AC =4,则△ADF周长为( ).

A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,连接
上,连接![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 是矩形.
是矩形.
![]() 小明在完成
小明在完成![]() 的证明后继续进行了探索,过点
的证明后继续进行了探索,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,得到四边形
,得到四边形![]() .此时,他猜想四边形
.此时,他猜想四边形![]() 是菱形.请在下列框图中补全他的证明思路.
是菱形.请在下列框图中补全他的证明思路.
小明的证明思路:由![]() ,
,![]() ,
,![]() 易证,四边形
易证,四边形![]() 是平行四边形.要证□
是平行四边形.要证□![]() 是菱形,只要证
是菱形,只要证![]() .由已知条件________,
.由已知条件________,![]() ,可证
,可证![]() ,故只要证
,故只要证![]() ,即证
,即证![]() ,易证________,________,故只要证
,易证________,________,故只要证![]() ,易证
,易证![]() ,
,![]() ,________,故得
,________,故得![]() ,即可得证.
,即可得证.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).

(1)作ΔABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标,
(2)作△ABC关于y轴对称的△A2B2C2,并写出点A2,B2,C2的坐标,
(3)观察点A1,B1,C1和A2,B2,C2的坐标,请用文字语言归纳点A1和A2,B1和B2,C1和C2坐标之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BCD的周长等于AB+BC;(4)D是AC中点其中正确的命题序号是_________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com