
【题目】如图,已知AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得到的关系中任选一个加以证明。
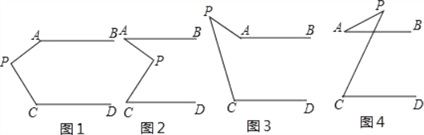
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是: .
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是: .
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是: .
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是: .
(5)在图 中,求证: .
【答案】答案见解析
【解析】试题分析:(1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案;
(4)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案.
试题解析:解:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
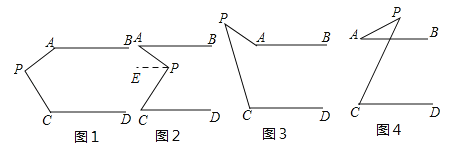
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
证明:过P点作PE∥AB,∴∠1=∠PAB.
又∵AB∥CD,PE∥CD,∴∠2=∠PCD,∴∠1+∠2=∠PAB+∠PCD,而∠APC=∠1+∠2,∴∠APC=∠PAB+∠PCD.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】八(1)班组织了一次汉字听写比赛,甲、乙两队各10人,其比赛成绩如下表(10分制):
甲队 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 9 | 9 | 8 |
乙队 | 7 | 7 | 8 | 9 | 10 | 10 | 9 | 10 | 10 | 10 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分.
(2)计算甲队的平均成绩和方差_
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
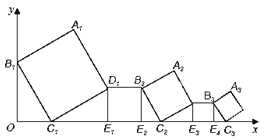
【题目】在平面直角坐标系中,正方形A1B1C1D1 、D1E1E2B2 、A2B2C2D2 、D2E3E4B3 、A3B3C3D3 ……按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3……在x轴上,已知正方形A1B1C1D1 的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……则正方形A2017B2017C2017D2017的边长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
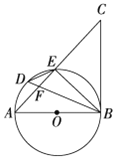
【题目】如图,AB是⊙O的直径,点D是弧AE上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF·DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
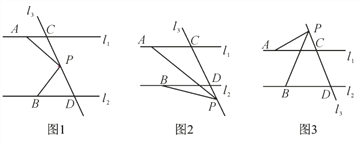
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P.
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试直接写出∠PAC,∠APB,∠PBD之间的关系,不必写理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,y1),B(﹣1,y2),C(3,y3)三点都在抛物线y=2x2﹣3的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1B.y1<y2<y3C.y2<y1<y3D.y3<y1<y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com