
【题目】如图,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于
于![]() 、
、![]() 两点,若反比例函数
两点,若反比例函数![]() 的图象与
的图象与![]() 有公共点,则
有公共点,则![]() 的取值范围是( )
的取值范围是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由点C的坐标结合直线AB的解析式可得出点A、B的坐标,求出反比例函数图象过点C时的k值,将直线AB的解析式代入反比例函数解析式中,令其根的判别式△≥0可求出k的取值范围,取其最大值,找出此时交点的横坐标,进而可得出此点在线段AB上,综上即可得出结论.
解:令y=x+5中x=1,则y=4,
∴B(1,4);
令y=x+5中y=2,则x=3,
∴A(3,2),
当反比例函数![]() (x>0)的图象过点C时,有2=
(x>0)的图象过点C时,有2=![]() ,
,
解得:k=2,
将y=x+5代入![]() 中,整理得:x25x+k=0,
中,整理得:x25x+k=0,
∵△=(5)24k≥0,
∴k≤![]() ,
,
当k=![]() 时,解得:x=
时,解得:x=![]() ,
,
∵1<![]() <3,
<3,
∴若反比例函数![]() (x>0)的图象与△ABC有公共点,则k的取值范围是2≤k≤
(x>0)的图象与△ABC有公共点,则k的取值范围是2≤k≤![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
【题目】一件工艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )
A.3.6 元
B.5 元
C.10 元
D.12 元
查看答案和解析>>
科目:初中数学 来源: 题型:
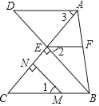
【题目】如图,BE⊥AC与点E,MN⊥AC于点N,∠1=∠2,∠3=∠C,若∠AFE=80°,求∠DAF的度数.请根据解题过程“填空”或“说明理由”.
解:∵BE⊥AC,MN⊥AC
∴BE∥MN
∴∠1= ( )
又∵∠1=∠2
∴∠2= ( )
∴EF∥BC( )
∵∠3=∠C
∴AD∥BC
∴AD∥EF
∴∠DAF+∠AFE=180°( )
∴∠DAF=180°﹣∠AFE=180°﹣80°=100°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法。
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a=________, b=___________.
)2,用含m、n的式子分别表示a、b,得a=________, b=___________.
(2)若a+4![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值。
)2,且a、m、n均为正整数,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() 与
与 ![]() 轴、
轴、 ![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与 ![]() 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,定点![]() 、
、![]() 、
、![]() 的坐标分别是(4,0)、(0,4)、(2,0),动点
的坐标分别是(4,0)、(0,4)、(2,0),动点![]() 在第一象限,且到原点
在第一象限,且到原点![]() 的距离为4个单位长度.
的距离为4个单位长度.
(1)当点![]() 到两坐标轴的距离相等时,求
到两坐标轴的距离相等时,求![]() 的面积;
的面积;
(2)若点![]() 是线段
是线段![]() (不与点
(不与点![]() 、
、![]() 重合)上的动点,当
重合)上的动点,当![]() 是等腰直角三角形时,求点
是等腰直角三角形时,求点![]() 到
到![]() 轴的距离.
轴的距离.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青少年“心理健康”问题已经引起了社会的关注,某中学对全校850名学生进行了一次“心理健康”知识测试,并从中抽取了50名学生的成绩(得分取正整数,满分为100分)作为样本,列出下面的频数分布表(单位:分)
成绩 | 50.5≤x<60.5 | 60.5≤x<70.5 | 70.5≤x<80.5 | 80.5≤x<90.5 | 90.5≤x<100.5 |
频数 | 2 | 8 | 10 | 16 | 14 |
(1)组距是 ,组数是 .
(2)成绩在60.5≤x<80.5范围的频数是 .
(3)画出频数分布直方图.
(4)若成绩在80分以上(不含80分)为优秀,试估计该校成绩优秀的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知3x=2y=5z≠0,求![]() 的值;
的值;
(2)某市政工程计划将安装的路灯交给甲、乙两家灯饰厂完成,已知甲厂生产100个路灯与乙厂生产150个路灯所用时间相同,且甲厂比乙厂每天少生产10个路灯,问甲、乙两家工厂每天各生产路灯多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com